Research for increasing the accuracy of the Leibniz formula for calculating the PI number and draw graphs
Introduction
There are many interesting ways to calculate the pi number: geometric constructions, natural experiments using random numbers, as well as a huge number of different formulas from simple to complex.
These methods are well researched and their characteristics are known, how much time and computing resources are needed to solve them.
It is always interesting to improve an existing method so that it works faster and easier.
Leibniz Formula
Basic Principles
The formula Madhava - Gregory - Leibniz is a simple sum of fractions of one divided by odd number from 1 to infinity. The sign of a fraction is changed at every step. For example, take the first number 1, the second number 1/3 with a minus sign, the third 1/5 with a plus sign, etc. It turns out the expression 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...
For an infinite number of terms, this sum is equal to the fourth part of pi. To get pi, we need to multiply the result by 4.
Using the Code
The simple program in C for calculating pi value:
double pi_4 = 0;
int n = 100;
int sign = 1;
int i = 0;
for (i = 1; i < n; i += 2)
{
if (sign)
{
pi_4 += 1.0 / i;
sign = 0;
}
else
{
pi_4 -= 1.0 / i;
sign = 1;
}
}
printf("PI = %.12f\n", pi_4 * 4);
In the for loop, the variable i changes from 1 to 99 by step of 2, that is, it takes values 1, 3, 5, 7, 9, etc. The value of n is greater by 1 than the maximum value of i in the loop. The variable sign changes the value at each step, and checking its value in the if condition, we determine to add or subtract the value (1 / i) to the result. The resulting value is multiplied by 4.
For a visual representation of the calculation process, we draw a graph for the Leibniz formula using the OpenGL library. Put the loop in the display function.
glBegin(GL_LINE_STRIP);
glColor3f(1, 1, 1);
for (i = 1; i < n; i += 2)
{
if (sign)
{
pi_4 += s / i;
sign = 0;
}
else
{
pi_4 -= s / i;
sign = 1;
}
glVertex3f(i, pi_4 * 4, 0);
}
glColor3f(1, 0, 1);
glVertex3f(n, pi_4 * 4 + 2. / n, 0);
glEnd();
We get the graph:
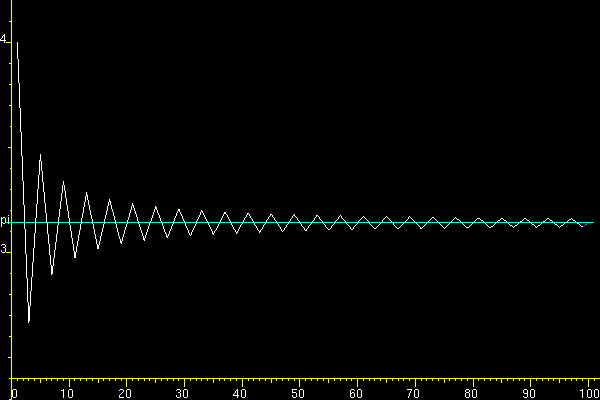
At each step, we get a value (white color) far from the pi line (blue color). To get the exact value, we need to continue the endless calculation process. How to get the result? It all depends on the goal.
Minimization Task
Our goal is to minimize deviation (red color) from the pi line (blue color) with a limited number of steps. At each step, the white line passes through the pi line. Half of the segment (red color) is closer to the line than its edges (white color). Thus, at each step, we get the maximum deviation (white color) from the line. This result is inverse to our goal of minimizing deviation.

Indian mathematician Madhava used correction terms to improve accuracy. We find the correcting terms empirically. Check the numerical value of the result for i from 1 to 99 (for n = 100) and compare it with the exact value of the pi number. For verification, use the value 4 arctan(1).
double pi = pi_4 * 4;
printf("PI = %.12f\n", pi);
printf("PI = %.12f\n", atan(1) * 4);
PI = 3.121594652591
PI = 3.141592653590
Please note that the numbers differ in a few digits. The first difference is (2 / n). Recall that n is an even number greater by 1 than the maximum value of i in the loop. Since the last term was with a minus sign, we add (2 / n).
pi = pi_4 * 4 + 2.0 / n;
Now the numbers will be like this:
PI = 3.141594652591
PI = 3.141592653590
The second difference is (2 / n3) or (2 / (n * n * n)). Now subtract (2 / n3) from the sum.
pi = pi_4 * 4 + 2.0 / n - 2.0 / (n * n * n);
Let's check what this is.
PI = 3.141592652591
PI = 3.141592653590
At least an accuracy greater than (1 / n3) is obtained, in contrast to the initial accuracy less than (1 / n).
Conclusion and Points of Interest
At first, I used very large values of n = 1,000,000,000 and waited a few seconds before getting the result. Then I divided the calculations into ten parallel threads and reduced n. Each thread gave its own amount, and then with a small n, I noticed that most of the digits match, with the exception of a few. I looked at the results at n = 100, 1000 and 10000 and found a (2 / n) difference. Upon careful examination, a second difference of (2 / n3) was found.
Of course, even with n = 100, the following differences are noticeable, but they need to be checked on exact numbers. It seems to me that two terms are enough to save computing resources. Indeed, to obtain the same accuracy by the usual method, it is necessary to calculate n4 terms.
So for the new n = 100,000,000, we get:
PI = 3.141592633590
PI = 3.141592653590
Here again, accuracy can be enhanced by the term (2 / n). Millions of terms are replaced by one. This is similar to obtaining a square wave using the sum of many harmonics of sine waves.
This study turned out to be useful and I turned to the search to find confirmation. I found a Wikipedia article called "Leibniz formula for pi".
In this article, I read that Indian mathematician Madhava used corrective terms to increase accuracy. I became convinced of the correctness of my research. I invite everyone to check the corrective terms that I have proposed. Maybe you will find new corrective terms with the help of exact calculations.
Corrective terms are useful to improve accuracy and save computing resources, especially in embedded systems and mobile devices.
It is interesting to use corrective terms in the tasks of digital signal processing.
Thanks for reading!
History
- 14th May, 2020: Initial version
Engineer of Automated Data Processing and Control Systems. Graduated from Novosibirsk State Technical University (NSTU), Department of Automation and Computers.
I worked in television and developed broadcast automation systems.
I write programs in C/C++, Java, PHP, JavaScript, HTML, XML, CSS, MySQL.
I am interested in software architecture. Architecture is art. I use the style of modernism, in particular, it is cubism. Means the desire to parse the problem into the simplest modules. This solution allows you to assemble complex systems that surpass the complexity of the initial design concepts. I am the author of this programming technique.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 







