Symbolic Integration with C#

• Download source (ZIP) - 1.8 MB
• Download source (RAR) - 1.7 MB

Introduction

Symbolic computation (computer algebra) is one of the computer science research areas. It deals with math formulae (expressions) and provides computer algorithms for manipulating the expressions in natural form, without reducing the expressions to numerical values. Mainly, symbolic computations used in special software, called Computer Algebra Systems (CAS). Modern computer algebra systems include a wide range of symbolic algorithms, from the simplification of complicated math formulae to dealing with partial differential equations describing various physical fields. The CAS software usually has Graphical User Interface (GUI) to show the results in natural mathematical form. One can use such software as a computer assistant that helps him to do routine operations with math formulae.

Nevertheless, there is a lot of software, besides the CAS, that need symbolic algorithms as one of its functionalities. For example, modern Computer-Aided Engineering (CAE) systems include a module of postprocessing. This module allows advanced processing of computational results got with the CAE system. One of the common realizations of the functionality is to provide the user-defined formula for processing. Thus, the software should include the tools for symbolic manipulations. The need for symbolic math modules also arises in many engineering, scientific and educational applications. The main function of such applications is not to provide a full range of symbolic math, but they should include some symbolic algorithms as a part of the software.

Two of the most interesting symbolic computations are differentiation and integration. These two operations have a lot in common. It should at least be noted that one of the powerful methods of integration is integration by parts. The method includes differentiation as one of the stages of the integration algorithm. On the other hand, symbolic integration is a much more difficult task than symbolic differentiation.

The article describes one of the possible simple symbolic integration approaches. This approach realized in the C# symbolic library ANALYTICS (can be downloaded from here). One of the advantages of the realization is that one can introduce new integration algorithms into the library without modifying core algorithms. The library can be easily embedded in C# applications and can provide many symbolic capabilities for the developing software.

Background

Let us first state the main difference between differentiation and integration from the algorithmic point of view. It will help us better understand the approach for realizing symbolic integration. A mathematical expression (formula) consists of constants (numbers, standard constants, such as Pi or Euler value), variables (commonly given names x, y, z and so on), algebraic operations (+, -, *, / and so on) and functions (sin, cos, ln, exp and so on). And what we can say about differentiation is that there is a straightforward recursive algorithm to get the derivative of any expression (if it exists). Why it is so? It is because we have such algorithms for every ingredient the expression consists of.

Consider the algebraic operations. We have differentiation rules for all of them. As an example, we know that derivative of a sum satisfies the following rule:

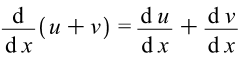
We know the product rule:

And there are differentiation rules for all types of algebraic operations, including powers and roots.

Then, consider functions. We know derivatives for most of the elementary transcendental and special functions. For composite functions (functions of functions) we have the chain rule of differentiation:

Thus, having formulae and rules of derivatives for all of the elements of expressions, we can provide an algorithm for differentiating any complicated expression.

Now, let us move next to the integration. Do we have rules of integration for all types of expressions? The answer is ‘No’. Let us consider the algebraic operations. Actually, we have integration rules only for two cases – multiplication by constant and integral of a sum:

We do not have a straightforward formula for other cases of algebraic operations such as multiplication, power, and others. Considering functions, we meet the same situation. We know the formulae of integrals for most of the elementary functions, but we have no integration rule for composite functions.

Summing it up, as opposed to symbolic differentiation, we cannot apply some straightforward recursive algorithm of symbolic integration. Instead of this, we should use special integration methods, such as integration by parts, integration by substitution, and others. The difference between integration rules and integration methods is very subtle. As a rule, as a method based on some formula. But the rule provides a straightforward formula, depending only on the type of expression. The formula can be applied to any expression of the type. On the other hand, a method of integration is sensitive to the elements the expression consists of. An integration method just points to one of the ways that can lead to the final integral of an expression. But we do not know which of the ways to choose. We need to analyze the internal ingredients of the expression to select the right way.

Integration Algorithm

What we are going to realize here is a symbolic integration algorithm. The algorithm must include the following capabilities:

• Realization of integration rules
• Realization of base integration formulae
• Interface for realizing integrals of functions
• Interface for realizing integration methods

The first point of the algorithm has been covered in the previous section. The second point assumes that we also must include in the integration engine such formulae as integral of ‘1/x’, ‘x^n’ and so on. We call them integration formulae, not integration rules, because they just define formulae of the integrals for concrete expressions. For example, the integral of ‘1/x’ with respect to ‘x’ is ‘ln(x)’. This is a formula, not a rule because we cannot apply this to the general expression ‘1/u(x)’. The last two points state that the realization of the algorithm must provide such an interface that would allow the addition of new formulae for function integrals and new advanced integration methods without modifying the core algorithm of integration.

Now it is time to see how to implement this algorithm in the ANALYTICS C# library. ANALYTICS is a general-purpose library for evaluating math formulae. One of the main components of the library is the ‘BaseExpression’ class that encapsulates base functionality for dealing with math expressions. Here is the class hierarchy of expressions:

Let us explain some of the classes that are of main interest for the theme of integration. The simple expressions in the hierarchy are literals (constants) and variables. We can easily realize the integration formulae for these expressions: integral of a constant ‘c’ by ‘x’ is ‘c*x’; integral of ‘x’ by ‘x’ is ‘x^2/2’.

All algebraic operations divided into unary operators and binary expressions. Unary operators stay for minus, factorial, and some others. We can realize the integration rule for the minus operator: just move the constant multiplier ‘-1’ over the integral. Let us note that the integral of the factorial operation ‘x!’ is not defined so we must include this occasion in the algorithm.

The binary operation expressions are the sequences of algebraic operations with two operands. An example of a sum expression is ‘x+sin(y)-1’. For this type of expression, the sum rule must be implemented, as described in the previous section. The product expression is a sequence of multiplications, for example, ‘A*x/2’. We must realize the integration rule for the product expression, namely, we must move the constant part of the expression, which does not depend on the integration variable, over the integral.

Some of the binary expressions cannot be integrated when depending on the integration variable. For example, there is no integral by ‘x’ for the following logical expression ‘x & y’. Some other binary expressions assume no integration rules, but they must provide an integration formula for the simple cases of the expression. For example, the power expression should realize integral formulae of ‘x^n’ and ‘a^x’.

Finally, the function expressions realize the concept of math functions, like sine, cosine, natural logarithm, and others. In the integration algorithm, we must provide the interface for function integrals. That is, we must be able to add the integration formula for any transcendental function, without the need to change the core integration algorithm. For all other complicated expressions, we must provide a similar interface of advanced integration methods that can be added to the integration engine.

The description of the algorithm sounds like something intricate, and indeed it is. Symbolic integration is not a trivial task. Let us consider the C# code, it will clarify the algorithm.

Realization

The described integration algorithm realized in the ‘Integrate’ method of the ‘BaseExpression’ class. Here is the partial code of the method, minor details omitted for clarity:

public virtual BaseExpression Integrate(string vName)
{
    BaseExpression result = null;

    if (!this.DependsOn(vName))
    {
        result = this * (new VariableExpression(vName));
        return result;
    }

    result = this.SelfIntegral(vName);

    if (result == null)
    {
        foreach (Integrator ii in Context.Integrals.ExpressionIntegrators)
        {
            result = ii.Integral(this, vName);
            if (result != null)            
            {
                return result;
            }
        }
    }

    return result;
}

The argument of the function ‘vName’ stays for the name of the integration variable. As the indefinite integral can be evaluated not for all expressions, we use the contract that the result is null when the algorithm fails to calculate the integral. Then we check if the expression depends on the variable, if not, we multiply the expression by the variable end return the result (it implements the formula for integral of a constant).

If the expression is not constant (with respect to the integration variable), we first call the ‘SelfIntegral’ method. This method implements the first three points of the integration algorithm, described in the previous section: integration rules; integration formulae for some simple expressions; integration formulae for functions. Calling this method brings the recursion here because integration rules and integration formulae realizations can call the ‘Integrate’ method. We will come back to this soon and consider the method for some simple cases.

The final part of the ‘Integrate’ method realizes the last point of the algorithm: it loops over all registered integrators and calls their ‘Integral’ method. If one of the integrators is able to evaluate the indefinite integral of the expression, we return it as the final result. The ‘Integrator’ is a special class for realizing advanced integration techniques. The ‘Integrator’ class has three descendants: ‘TemplateIntegrator’ – realizes integration formula for an expression, matching some template; ‘SimplifyIntegrator’ – simplifies the expression first and then calls the ‘Integrate’ method for the new expression; and ‘AlgorithmIntegrator’ – realizes general integration methods, such as integration by parts and so on.

Let us return back to the ‘SelfIntegral’ method and consider its realization for several expression types. Here is the C# code of the method for the ‘UnaryOperatorExpression’ class (again, some part of the code reduced to give better clarity):

protected override BaseExpression SelfIntegral(string vName)
{
    BaseExpression result = null;
    OperatorType t = Utilities.GetOperatorType(Sign, OperatorArity.Unary);

    switch (t)
    {
        case OperatorType.Minus:
        {
            BaseExpression opndi = operand.Integrate(vName);
            if (opndi != null)
            {
                result = -opndi;
            }
            break;
        }

        case OperatorType.Factorial:
        {
            throw new ExpressionTypeIntegralException(Sign, Reconstruct());
        }
        
        // ... other unary operators
    }

    return result;
}

One can see in the code how this method realizes the integration rule for the minus operator: first, it tries to integrate the operand of the expression; if the integral found (not null), it then negated to get the final result (the ANALYTICS library overloads algebraic C# operators, such as +, -, *, /, to simplify manipulations with expression objects in the code). For example, if the original expression is ‘-x’, the operand is ‘x’. The integral of the operand is ‘1/2*x^2’, and the final result is ‘-1/2*x^2’. On the other hand, when trying to integrate a factorial expression (for example ‘x!’), we get the exception because the integral cannot be evaluated in this case.

Now let us look at the code of the method for the ‘SumExpression’ class:

protected override BaseExpression SelfIntegral(string vName)
{
    List<BaseExpression> integrals = new List<BaseExpression>();
    foreach (BaseExpression operand in operands)
    {
        BaseExpression i = operand.Integrate(vName);
        if (i == null)
        {
            return null;
        }

        integrals.Add(i);
    }

    BaseExpression result = new SumExpression("", operators, integrals);
    return result;
}

The code realizes the sum rule of integration. It first finds the integrals for all operands, and if the integrals successfully evaluated, a new sum expression with the same operators returned as the final result. For example, let us have the following sum expression ‘x+1-1/x+A’. The operands here are ‘x’, ‘1’, ‘1/x’, and ‘A’ and the operators are ‘+’, ‘-‘, ‘+’. Thus, we will get the following integrals of the operands: ‘1/2*x^2’, ‘x’, ‘ln(x)’, and ‘A*x’. Then we will create a new sum expression with the three operators and get the final result as ‘1/2*x^2+x-ln(x)+A*x’.

Analogously, all other operator expressions realize integration rules and formulae if possible. We hope that the idea of the integration method realization is clear and we do not give here the code for all expression classes. One thing left is how to introduce integration formulae for functions and how to introduce advanced integration algorithms. We will explain it a little bit later and now we will show some examples of symbolic integration.

Symbolic Integration Examples

The base functionality of symbolic integration in the ANALYTICS library realized via the simple interface of the ‘Translator’ class. Here is the C# code template for the common use of the interface:

string f = inputTextBox.Text;
try
{
    if (translator.CheckSyntax(f))
    {
        string F = translator.Integral(f, "x");

        // show the result integral F
    }
}
catch (Exception ex)
{
    // process the exception
}

Here ‘f’ is the integrand expression; ‘translator’ is an instance of the ‘Translator’ class, and ‘F’ is the evaluated indefinite integral expression. To show the result in natural math form, we will use the approach, described in the article ‘Drawing and Evaluating Math Formulae in WPF Applications’.

What types of expressions can we integrate with the realized algorithm? The algorithm supports all integration rules and several integration formulae for algebraic expressions. It does not support integrals of functions and advanced integration methods.

First, let us evaluate the integral of the simple polynomial ‘A*x^2+B*x+C’. Here is the integration result:

As was expected, the algorithm successfully evaluated the integral. At the first step, it used the rule of sum integral; then it applied another integration rule for all of the sum operands – move a constant over the integral; finally, the power integral formula (integral of ‘x^n’ is ‘x^(n+1)/(n+1)’) was deployed.

Now, let us try to calculate the integral of a little bit more complicated rational expression ‘A/x^3+B/(k*x+b)^2-1/x’. And we get the following result:

We can see from the resulting formula that there are some advanced integration rules, realized in the algorithm. First, the algorithm is able to convert the rational expression to the power (for example, ‘A/x^3’ converted to ‘A*x^-3’) and then apply the appropriate integration formula. Second, it is able to work with linear expressions of the argument, namely ‘k*x+b’, and, again, use the appropriate formula.

Let us show how the algorithm works with the expressions containing rational powers, like this ‘A*x^(1/2)+B*x^(-3/4)’:

Note, how the algorithm keeps the powers in the rational form for more convenient representation.

Another type of supported expressions is exponentials. For example, integrating the expression ‘a^x/2+B*e^-x-C/a^(k*x+b)’ we get the following output:

One can see that here the algorithm also supports linear expressions of the variable as exponents ‘k*x+b’. It also recognizes standard named constants, like ‘e’ and ‘Pi’.

Can we integrate some more complicated expressions? What about this one ‘x*a^x’? The expression consists of two elements, ‘x’ and ‘a^x’, any of which can be easily handled with the algorithm. Unfortunately, this expression cannot be integrated with the algorithm realizing only integration rules and base integration formulae. It is because there is no integration rule for general product expression. We need to realize advanced integration methods for special cases of products.

Extending Integration Capabilities

We see that the core integration algorithm, using only integration rules and base integration formula, is able to handle a rather limited range of math expressions. But as was mentioned above, this algorithm includes the part that allows extending the integration capabilities: introduce function integration formulae and advanced integration methods.

The approach introducing a function integration formula is very simple: we need to realize a descendent of the special function integrator. As the class realized, the core integration algorithm automatically finds the class (with the C# reflection mechanisms) and uses it in the appropriate situations.

For example, consider the realization of the integration formula for two trigonometric functions – sine and cosine:

public sealed class SineIntegral : SimpleFunctionalIntegral
{
    public override BaseExpression BaseIntegral(BaseExpression arg)
    {
        BaseExpression result = FunctionExpression.CreateSimple(Names.Cosine, arg);
        result = UnaryOperatorExpression.Negate(result);
        return result;
    }

    public override string GetFunctionName()
    {
        return Names.Sine;
    }
}

public sealed class CosineIntegral : SimpleFunctionalIntegral
{
    public override BaseExpression BaseIntegral(BaseExpression arg)
    {
        BaseExpression result = FunctionExpression.CreateSimple(Names.Sine, arg);
        return result;
    }

    public override string GetFunctionName()
    {
        return Names.Cosine;
    }
}

The descendant classes override two methods of the base functional integral class. The ‘GetFunctionName’ method returns the name of the function to integrate. The ‘BaseIntegral’ method makes the expression that is the integral of the function with respect to the ‘arg’ variable. The rest of the rough work is done by the core integration algorithm and base class.

Now we can integrate simple expressions, containing sine and cosine functions, as shown below:

Again, one can see that the algorithm is able to deal with not only simple ‘sin(x)’ and ‘cos(x)’ functions, but also with the functions of liner arguments. This rule is embedded into the core algorithm. Unfortunately, we still cannot integrate functions of nonlinear arguments, for example ‘sin(x^2)’. We need to implement special integration methods. This task is the most complicated and mercurial part of the work. Let us show the simplest example of an integrator class that can extend the range of expressions to integrate. Here is the code of the class:

public sealed class ExpandIntegrator : SimplifyIntegrator
{
    protected override BaseExpression Simplify(BaseExpression expr, string vName)
    {
        if (expr is BinaryOperationsExpression)
        {
            BinaryOperationsExpression be = (BinaryOperationsExpression)expr;
            if (be.OperationCount > 0)
            {
                if (be.CanExpand())
                {
                    BaseExpression ee = be.Expand();
                    if (ee != null)
                    {
                        ee.Simplify();
                        return ee;
                    }
                }
            }
        }

        return null;
    }
}

The class is inherited from the ‘SimplifyIntegrator’, and it tries to simplify the expression in the sense of the integration process. Namely, the method expands a binary expression. For example, the power expression ‘(A*x+B)^2’ will be simplified to the following ‘A^x^2+2*A*B*x+C^2’ which can be successfully processed with the core algorithm. Having realized the class, we are able to integrate the following expression ‘(A*x+B)^2*(C*x-D)’:

Analogously, we can provide more advanced methods of integration to the system. Their realization is out of the article’s scope. The main idea here is that it can be done without the need to modify the core algorithm. Once one advanced integration method is realized, it will be accessible to the core algorithm, extending the capabilities of the symbolic integration.

Conclusions

This article introduced one approach for symbolic integration algorithm with C#. The approach implemented in the ANALYTICS library. The core integration algorithm realizes all integration rules and base integration formulae for unary and binary algebraic operators and functions. Additional advanced integration formulae and methods can be easily introduced to the algorithm by providing descendants of special classes. The system automatically finds the advanced integrators and uses them for the appropriate math expressions, providing new integration capabilities. As the library is entirely written in C#, it does require no additional math packages. The library can be easily integrated into any .NET application, bringing symbolic integration capabilities to scientific, engineering, and educational software.

History

• 31^st January, 2021: Initial version