Simple Fast Adaptive Grid to Accelerate Collision Detection between AABB of Particles
A walkthrough for a grid implementation of "particle in cell" problem to improve performance of axis-aligned bounding-box (AABB) collision checking in various scenarios
Collision Detection
Collision detection is the act of finding intersections of multiple objects in a dimension or in higher number of dimensions. As it sounds simple while talking, it is very useful in multiple branches of science, video games and web sites. A popular use case is keeping rigid bodies from moving into each other's volume in a video game's physics simulation.
Background
In coding for a simple physics simulation or writing some tutorial for a graphics-related problem, developers may require a collision-detection algorithm, but many include a whole fully-fledged game-engine (as large as 100s of megabytes) only to use it as a collision detector and go through long installation & dependency compilation phases. It may be useful to have a less-than-1000-line header-only solution and simply "#include" the header, that does only AABB collision detection for many particles (and preferably fast enough for real-time work) and nothing more.
Baseline
Before starting optimizations, there is a given challenge (with simplified edge-cases handling):
- Detect all-pairs collisions between 10k point-cloud object instances,
- each cloud object made of 125 points (3 floating-point variables each)
- randomly sized
- randomly distributed on 3D space
- Do same, but at 60 FPS (crude definition of real-time)
- Detect collisions between 1 dynamic point cloud AABB vs 10k static point-cloud AABBs, quicker than 1 microsecond
- Use a low-end system (FX8150 CPU at 2.1 GHz, single-channel 1333MHz DDR3 RAM)
- In C++ (g++-10 for Ubuntu)
As a simplest reference solution (to be the base of performance comparisons), program will have a highly simplified brute-force intersection test:
// psudo-code
CollisionList collisionPairList;
for(each a object in scene)
for(each b object in scene)
for(each c point in a)
for(each d point in b)
{
if(c is close enough to d)
{
// a intersects b
add id-values of a and b into collisionPairList
end the loops of c and d
}
}
Reference test program source code (uses the FastCollisionDetectionLib.h header file from this github repository):
#include"FastCollisionDetectionLib.h"
#include<iostream>
template<typename CoordType>
struct Vector3D
{
CoordType x,y,z;
Vector3D<CoordType> crossProduct(Vector3D<CoordType> vec)
{
Vector3D<CoordType> res;
res.x = y*vec.z - z*vec.y;
res.y = z*vec.x - x*vec.z;
res.z = x*vec.y - y*vec.x;
return res;
}
Vector3D<CoordType> operator - (Vector3D<CoordType> vec)
{
Vector3D<CoordType> result;
result.x = x-vec.x;
result.y = y-vec.y;
result.z = z-vec.z;
return result;
}
Vector3D<CoordType> operator + (Vector3D<CoordType> vec)
{
Vector3D<CoordType> result;
result.x = x+vec.x;
result.y = y+vec.y;
result.z = z+vec.z;
return result;
}
Vector3D<CoordType> operator * (CoordType v)
{
Vector3D<CoordType> result;
result.x = x*v;
result.y = y*v;
result.z = z*v;
return result;
}
// warning: sqrt is not necessary in production code like:
// if ( v1.abs()<v2.abs() ) { .. }
// the sqrt below is intentionally left to simulate "heavy" task in "challenge 1"
CoordType abs()
{
return std::sqrt(x*x+y*y+z*z);
}
};
template<typename CoordType>
struct PointCloud
{
Vector3D<CoordType> point[125];
PointCloud(CoordType x, CoordType y, CoordType z)
{
for(int i=0;i<125;i++)
{
point[i].x=x+i%5-2.5f;
point[i].y=y+(i/5)%5-2.5f;
point[i].z=z+i/25-2.5f;
}
}
};
template<typename CoordType>
bool pointCloudIntersection(PointCloud<CoordType>& cl1, PointCloud<CoordType>& cl2)
{
for(Vector3D<CoordType>& p:cl1.point)
{
for(Vector3D<CoordType>& p2:cl2.point)
{
if((p-p2).abs()<1.0f)
{
return true;
}
}
}
return false;
}
int main()
{
using cotype = float;
bool results[41*41];
PointCloud<cotype> ico1(0,0,0);
// heating the CPU for benchmarking
for(int i=0;i<10000;i++)
{
PointCloud<cotype> ico2(0,0.1f,i*0.1f);
results[0]=pointCloudIntersection(ico1,ico2);
}
// benchmark begin
size_t nano;
{
FastColDetLib::Bench bench(&nano);
for(int j=-20;j<=20;j++)
for(int i=-20;i<=20;i++)
{
PointCloud<cotype> ico2(0,i*0.5f,j*0.5f);
results[i+20+(j+20)*41 ]=pointCloudIntersection(ico1,ico2);
}
}
std::cout<<41*41<<"x collision checks between 2 clouds =
"<<nano<<" nanoseconds ("<<(nano/(41.0*41.0))<<" ns per collision check)"<<std::endl;
for(int i=0;i<41*41;i++)
{
if(i%41==0)
std::cout<<std::endl;
std::cout<<results[i];
}
std::cout<<std::endl;
return 0;
}
As expected, the program outputs the below result:
1681x collision checks between 2 clouds = 253073988 nanoseconds
(150550 ns per collision check)
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000111111111111111111100000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
00000000000000000000000000000000000000000
Every point-cloud vs point-cloud collision-check takes 150 microseconds. On the next test, collision detection for 100 point-clouds is computed:
int main()
{
using cotype = float;
PointCloud<cotype> ico1(0,0,0);
// heating the CPU for benchmarking
for(int i=0;i<10000;i++)
{
PointCloud<cotype> ico2(0,0.1f,i*0.1f);
pointCloudIntersection(ico1,ico2);
}
const int N = 100;
std::vector<PointCloud<cotype>> objects;
for(int i=0;i<N;i++)
{
objects.push_back(PointCloud<cotype>(i*1.5,i*1.5,i*1.5));
}
// benchmark begin
size_t nano;
std::map<int,std::map<int,bool>> collisionMatrix;
{
FastColDetLib::Bench bench(&nano);
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
{
collisionMatrix[i][j]=pointCloudIntersection(objects[i],objects[j]);
}
}
std::cout<<N*N<<"x collision checks between 2 clouds =
"<<nano<<" nanoseconds ("<<(nano/((double)N*N))<<" ns per collision check)"<<std::endl;
std::cout<<collisionMatrix.size()<<" unique object are in a collision"<<std::endl;
return 0;
}
The result is as follows:
10000x collision checks between 2 clouds = 1002381391 nanoseconds
(100238 ns per collision check)
100 unique object are in a collision
Same test with N=500:
250000x collision checks between 2 icosahedrons = 25975908607 nanoseconds
(103904 ns per collision check)
500 unique object are in a collision
Run-time increased from 1 second to 26 seconds (despite 1 collision computation lowered to 103 microseconds). At this scaling rate ( O(N^2) ), 10k point clouds need no less than 3 hours. This is not close enough to real-time performance.
First Optimization: AABB
To evade unnecessary collision checking (such as between object 1 and object 100 in test above), axis-aligned bounding-box of each object can be computed and used for "approximation" of collision checking such that it makes it safe to say "these two objects are certainly not overlapping" depending on AABB collision test result (false). If AABB collision returns true, then it will be useful to do check the finer grained point-cloud vs point-cloud collision.
AABB requires only simple min-max points in 3D space for each object, for every axis X,Y and Z.
- minimum X: the minimum X coordinate of all points in the object that makes first contact in X dimension
- maximum X: the maximum X coordinate of all points in the object that makes first contact in X dimension
- same for Y and Z
Axis-aligned bounding-buffer collision checking is simple:
- Check if two object AABBs collide on X dimension (projection on X axis)
- if they don't collide, there is no collision
- Do same checking for Y and Z dimensions
- If all axis have collision, then there is collision between AABBs
The following function can be repeatedly used for X, Y and Z dimensions of two AABBs to find a collision:
bool intersectDim(
const CoordType minx, const CoordType maxx,
const CoordType minx2, const CoordType maxx2)
{
return !((maxx < minx2) || (maxx2 < minx));
}
New point cloud class is given extra boundary calculations:
template<typename CoordType>
struct PointCloud
{
CoordType xmin,ymin,zmin;
CoordType xmax,ymax,zmax;
Vector3D<CoordType> point[125];
PointCloud(CoordType x, CoordType y, CoordType z)
{
xmin=x-2.5f;
ymin=y-2.5f;
zmin=z-2.5f;
xmax=x-2.5f;
ymax=y-2.5f;
zmax=z-2.5f;
for(int i=0;i<125;i++)
{
point[i].x=x+i%5-2.5f;
point[i].y=y+(i/5)%5-2.5f;
point[i].z=z+i/25-2.5f;
if(xmin>point[i].x)
xmin=point[i].x;
if(ymin>point[i].y)
ymin=point[i].y;
if(zmin>point[i].z)
zmin=point[i].z;
if(xmax<point[i].x)
xmax=point[i].x;
if(ymax<point[i].y)
ymax=point[i].y;
if(zmax<point[i].z)
zmax=point[i].z;
}
}
};
New 3D collision test, still brute-force but evading unnecessary checks by broad-phase collision check:
std::map<int,std::map<int,bool>> collisionMatrix;
{
FastColDetLib::Bench bench(&nano);
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
{
// check AABB collision on X axis
if(intersectDim(objects[i].xmin,objects[i].xmax,objects[j].xmin,objects[j].xmax))
// check AABB collision on Y axis
if(intersectDim(objects[i].ymin,objects[i].ymax,objects[j].ymin,objects[j].ymax))
// check AABB collision on Z axis
if(intersectDim(objects[i].zmin,objects[i].zmax,
objects[j].zmin,objects[j].zmax))
// only then, real fine-grained collision-checking is made
collisionMatrix[i][j]=pointCloudIntersection(objects[i],objects[j]);
}
}
The output (for 500 point-clouds again, with same initializations) is as below:
250000x collision checks between 2 clouds = 55842744 nanoseconds
(223.371 ns per collision check)
500 unique object are in a collision
Decreasing run-time from 26 seconds to 55 milliseconds is very helpful on the way to real-time performance but still not enough.
At this point, scale of benchmark can be increased again, the below output is from the same test ran for 10000 particles:
100000000x collision checks between 2 clouds = 2015666583 nanoseconds
(20.1567 ns per collision check)
10000 unique object are in a collision
2 seconds of run-time for 10k objects is only 59.5 FPS far from real-time performance. AABB collision checking is useful for early-exiting from collision checking. If X-dimension check fails, all the other dimension calculations are evaded. Since processing a sorted array is faster due to branch-prediction of CPU, the initialization of point-clouds on increasing X dimension is also helping here. For a pseudo-random distribution, it is not wrong to expect a lower performance.
Performance with random distribution (source code):
100000000x collision checks between 2 clouds = 20054203334 nanoseconds
(200.542 ns per collision check)
10000 unique object are in a collision
It has only 1/10 speed compared to a sorted array of AABB of objects. Even an old CPU like FX8150 takes speculation serious and maintains 10x performance with sorted arrays, at least when run-time is dominated by branching.
This means, for real-world scenarios (with randomness), it is currently only 0.05 FPS, or 59.95 FPS away from real-time performance and indicates the need for a spatial acceleration structure.
Second Optimization: Grid
There are multiple types of acceleration-structures that are better on their application areas and have specific disadvantages.
- Uniform Grid: Divides volume into single 3D layer of cells to store objects that touch them.
- Advantage: Performs good when object density is uniform across the computed volume.
- Disadvantage: Teapot-in-stadium problem causes uniform grid to waste too high memory unused and lose efficiency for computing colllisions.
- Octree: Divides volume into fixed hierarchical volumes made of 8 child-nodes per parent-node.
- Advantage: irregular object density is handled much better than a uniform grid, reducing memory footprint.
- Disadvantage: tree-traversal latency
- Kd-Tree: Similar to octree but division is maintained as dual child-nodes per parent-node
- Advantage: Closest neighbor search is faster
- Disadvantage: Requires extra time to rebalance when adding/removing objects
- BVH: Divides groups objects instead of volume.
- Advantage: Nodes have no bounds, they can map practically an infinite volume.
- Disadvantage: Nodes can overlap, even between child-node and parent-node, this makes it harder to compute closest neighbors or other attributes that use "spatial hashing".
In this article, the simplest spatial acceleration, uniform grid structure, is implemented, benchmarked against brute-force and optimized to become adaptive.
Implementing a grid is straightforward, with two different versions:
- Grid of collision masks
- Create an array of integers and reinterpret them as cells of an imaginary grid of a volume.
- For each object, put its pointer or id value into all overlapping cells in the grid
- For every other object, check id values / pointers found only in overlapping cells
- Compute collisions only within cells that have least 1 object id
- Grid of center points
- Create an array of integers and reinterpret them as cells again
- For each object, put id value only to the cell that contains the center of AABB
- For every other object, scan all neighboring cells that may contain an object's id
These implementations have different performance characteristics. Using only center points to insert id value saves more memory and insertion operation takes less time. Using collision masks makes collision query faster if objects are smaller than a cell. Center point variant does not work efficiently when there are various shaped objects with different AABB sizes. This forces the grid to scan for cells over a greater distance due to find bigger objects' collisions. Collision masking on the other hand, signs only the cells that overlap with the object AABB regardless of its size and is still maintain speed if high percentage of objects are small enough.
In short definition, collision mask gives greater collision scanning performance for the grid while center point version has much better object-insertion performance.
The test implementation will be using collision mask version of the uniform grid:
- Finding a list of overlapping cells is O(1) operation
- Traversing overlapping cells (to insert id value) is O(k) where k=number of overlapping cells
- Computing collisions by brute-force is O(m*m) where m=maximum number of particles in cell
- Overall complexity becomes O(N*k*m*m)
- If objects are smaller than cells, it becomes O(N*m*m)
- If cells are given only small number of objects, it becomes O(N) with a constant
Grid Implementation
By offloading AABB-related calculations from PointCloud to AABBofPointCloud struct (source code), it becomes easier to work with different objects later, but for simplicity, interface declarations are postponed to later titles and only simple struct wrapper is used.
New point cloud struct:
template<typename CoordType>
struct PointCloud
{
Vector3D<CoordType> point[125];
PointCloud(CoordType x, CoordType y, CoordType z)
{
for(int i=0;i<125;i++)
{
point[i].x=x+i%5-2.5f;
point[i].y=y+(i/5)%5-2.5f;
point[i].z=z+i/25-2.5f;
}
}
};
AABB struct:
template<typename CoordType>
struct AABBofPointCloud
{
AABBofPointCloud(int idPrm, PointCloud<CoordType> * pCloudPrm)
{
id=idPrm;
pCloud = pCloudPrm;
xmin=pCloud->point[0].x;
ymin=pCloud->point[0].y;
zmin=pCloud->point[0].z;
xmax=pCloud->point[0].x;
ymax=pCloud->point[0].y;
zmax=pCloud->point[0].z;
for(int i=0;i<125;i++)
{
if(xmin>pCloud->point[i].x)
xmin=pCloud->point[i].x;
if(ymin>pCloud->point[i].y)
ymin=pCloud->point[i].y;
if(zmin>pCloud->point[i].z)
zmin=pCloud->point[i].z;
if(xmax<pCloud->point[i].x)
xmax=pCloud->point[i].x;
if(ymax<pCloud->point[i].y)
ymax=pCloud->point[i].y;
if(zmax<pCloud->point[i].z)
zmax=pCloud->point[i].z;
}
}
int id;
PointCloud<CoordType>* pCloud;
CoordType xmin;
CoordType ymin;
CoordType zmin;
CoordType xmax;
CoordType ymax;
CoordType zmax;
};
Grid class:
template<typename CoordType, int Size, int ObjectsPerCell>
class Grid
{
public:
Grid(CoordType minCor, CoordType maxCor)
{
id=0;
mincorner=minCor;
maxcorner=maxCor;
cellData.resize(Size*Size*Size*(ObjectsPerCell+1));
for(int i=0;i<cellData.size();i++)
cellData[i]=0;
}
template<typename Func>
void forEachCellColliding(AABBofPointCloud<CoordType>* aabb, const Func& func)
{
// calculate cell size (equal for all dimensions for now)
const CoordType step = (maxcorner - mincorner)/Size;
// calculate overlapping region's cell indices
const int mincornerstartx = std::floor((aabb->xmin - mincorner) / step);
const int maxcornerendx = std::floor((aabb->xmax - mincorner) / step);
const int mincornerstarty = std::floor((aabb->ymin - mincorner) / step);
const int maxcornerendy = std::floor((aabb->ymax - mincorner) / step);
const int mincornerstartz = std::floor((aabb->zmin - mincorner) / step);
const int maxcornerendz = std::floor((aabb->zmax - mincorner) / step);
for(int i=mincornerstartz;i<=maxcornerendz;i++)
for(int j=mincornerstarty;j<=maxcornerendy;j++)
for(int k=mincornerstartx;k<=maxcornerendx;k++)
{
if(i<0 || i>=Size || j<0 || j>=Size || k<0 || k>=Size)
continue;
func(k,j,i,aabb);
}
}
void addObject(AABBofPointCloud<CoordType>* aabb)
{
forEachCellColliding
(aabb, [&](int k, int j, int i, AABBofPointCloud<CoordType>* aabb){
const int collidingCellIndex = (k+j*Size+i*Size*Size)*(ObjectsPerCell+1);
const int lastUsedIndex = cellData[collidingCellIndex]++;
cellData[collidingCellIndex+lastUsedIndex+1]=id;
idMapping[id++]=aabb;
});
}
std::vector<AABBofPointCloud<CoordType>*>
checkCollisionsWithSingleAABB(AABBofPointCloud<CoordType>* aabb)
{
std::vector<AABBofPointCloud<CoordType>*> result;
forEachCellColliding
(aabb, [&](int k, int j, int i, AABBofPointCloud<CoordType>* aabb){
const int collidingCellIndex = (k+j*Size+i*Size*Size)*(ObjectsPerCell+1);
const int numObjectsInCell = cellData[collidingCellIndex];
for(int p=0;p<numObjectsInCell;p++)
{
const int idObj = cellData[collidingCellIndex+1+p];
AABBofPointCloud<CoordType>* aabbPtr = idMapping[idObj];
// evade self-collision and duplicated collisions
if( aabb->id < aabbPtr->id)
if(intersectDim(aabb->xmin, aabb->xmax, aabbPtr->xmin, aabbPtr->xmax))
if(intersectDim(aabb->ymin, aabb->ymax, aabbPtr->ymin, aabbPtr->ymax))
if(intersectDim
(aabb->zmin, aabb->zmax, aabbPtr->zmin, aabbPtr->zmax))
{
result.push_back(aabbPtr);
}
}
});
return result;
}
private:
int id;
CoordType mincorner,maxcorner;
std::map<int,AABBofPointCloud<CoordType>*> idMapping;
std::vector<int> cellData;
};
Both object insertion and collision checking are using the same base function that scans over all overlapping cells and only the innermost part is changed between the insertion and checking, by a lambda function.
Please note that all duplicated calculations and self-collisions are evaded by a simple id comparison before collision tests. This effectively gives 2x performance even without any optimization.
Due to uniform grid requires uniform distribution, object distribution area is increased to a cube of width 450 while each point cloud has size of 5 units. With 10000 clouds:
const int N = 10000;
std::vector<PointCloud<cotype>> objects;
oofrng::Generator<64> gen;
for(int i=0;i<N;i++)
{
objects.push_back(PointCloud<cotype>(gen.generate1Float()*450,
gen.generate1Float()*450,gen.generate1Float()*450));
}
std::vector<AABBofPointCloud<cotype>> AABBs;
for(int i=0;i<N;i++)
{
AABBs.push_back(AABBofPointCloud<cotype>(i,&objects[i]));
}
// benchmark begin
size_t nano;
std::map<int,std::map<int,bool>> collisionMatrix;
{
FastColDetLib::Bench bench(&nano);
// uniform grid for 32x32x32 cells each with 30 objects max
// mapped to (0,0,0) - (450,450,450) cube
Grid<cotype,32,30> grid(0,450);
// add AABBs to grid
for(int i=0;i<N;i++)
{
grid.addObject(&AABBs[i]);
}
for(int i=0;i<N;i++)
{
std::vector<AABBofPointCloud<cotype>*> collisions =
grid.checkCollisionsWithSingleAABB(&AABBs[i]);
for(AABBofPointCloud<cotype>* aabb:collisions)
{
if(pointCloudIntersection(*aabb->pCloud, *AABBs[i].pCloud))
{
collisionMatrix[AABBs[i].id][aabb->id]=true;
collisionMatrix[aabb->id][AABBs[i].id]=true;
}
}
}
}
std::cout<<N<<" vs "<<N<<" point-clouds collision checking by uniform grid=
"<<nano<<" nanoseconds"<<std::endl;
int total = 0;
for(auto c:collisionMatrix)
{
for(auto c2:c.second)
{
if(c2.second)
total++;
}
}
std::cout<<total<<" total collisions (half as many for pairs)"<<std::endl;
The output is as shown below:
10000 vs 10000 point-clouds collision checking by uniform grid= 32221053 nanoseconds
564 total collisions (half as many for pairs)
32 milliseconds per 10000 vs 10000 collision test is very close to the 60 FPS target (16.6 ms) and not too far from 1 microsecond per dynamic collision check (3.2 microsecond per cloud currently).
For simple grid implementations, tuning is required to achieve best performance for a specific scene. The above test uses a grid of 32x32x32 cells and maximum 30 objects per cell. To have an idea about best performance, the latency of pointCloudUntersection(p1,p2) function must be subtracted from total latency. Commenting this function call out results in 18 milliseconds of run-time. This means that on the grid-side, there is 14 milliseconds of headroom to optimize. This can be achieved by tuning grid parameters, memory access pattern, types of data to be saved on cells.
Filling a grid and doing collision tests for each AABB versus whole grid one by one is most probably thrashing the cache contents of CPU. By the time second AABB is tested, the first AABB's traversed cell data is replaced. To fix this issue, tiled-computing is needed. Tiling size needs to be at most the size of L1 cache of CPU to benefit from fastest cell data access.
Since each cell was given a limit of 30 AABBs to store, running brute-force on each cell could use L1 cache efficiently without increasing time-complexity beyond unacceptable levels, if there are not many duplicates of cell contents.
With a new method for Grid class (source code), collision-test algorithm iterates over cells instead of AABBs and does basic duplicate-removal by maintaining an internal collision matrix:
std::map<int,std::map<int,bool>> checkCollisionAllPairs()
{
std::map<int,std::map<int,bool>> collisionMatrix;
for(int k=0;k<Size;k++)
for(int j=0;j<Size;j++)
for(int i=0;i<Size;i++)
{
const int cellIndex = (i+j*Size+k*Size*Size)*(ObjectsPerCell+1);
const int nAABB = cellData[cellIndex];
// no check if only 1 or less AABB found
if(nAABB<2)
continue;
// evading duplicates
for(int o1 = 0; o1<nAABB-1; o1++)
{
for(int o2 = o1+1; o2<nAABB; o2++)
{
AABBofPointCloud<CoordType>* aabbPtr1 =
idMapping[cellData[cellIndex+1+o1]];
AABBofPointCloud<CoordType>* aabbPtr2 =
idMapping[cellData[cellIndex+1+o2]];
if( aabbPtr1->id < aabbPtr2->id)
if(intersectDim(aabbPtr1->xmin, aabbPtr1->xmax,
aabbPtr2->xmin, aabbPtr2->xmax))
if(intersectDim(aabbPtr1->ymin, aabbPtr1->ymax,
aabbPtr2->ymin, aabbPtr2->ymax))
if(intersectDim(aabbPtr1->zmin, aabbPtr1->zmax,
aabbPtr2->zmin, aabbPtr2->zmax))
{
collisionMatrix[aabbPtr1->id][aabbPtr2->id]=true;
}
}
}
}
return collisionMatrix;
}
This allows only a simple change in the benchmarking algorithm to do same work, faster:
size_t nano;
std::map<int,std::map<int,bool>> collisionMatrixTmp;
std::map<int,std::map<int,bool>> collisionMatrix;
{
FastColDetLib::Bench bench(&nano);
// uniform grid for 16x16x16 cells each with 30 objects max
// mapped to (0,0,0) - (450,450,450) cube
Grid<cotype,16,30> grid(0,450);
// add AABBs to grid
for(int i=0;i<N;i++)
{
grid.addObject(&AABBs[i]);
}
collisionMatrixTmp = grid.checkCollisionAllPairs();
for(auto c:collisionMatrixTmp)
{
for(auto c2:c.second)
{
if(c2.second)
if(pointCloudIntersection(*AABBs[c.first].pCloud,*AABBs[c2.first].pCloud))
{
collisionMatrix[c.first][c2.first]=true;
collisionMatrix[c2.first][c.first]=true;
}
}
}
}
The output is as below:
10000 vs 10000 point-clouds collision checking by uniform grid= 22510565 nanoseconds
564 total collisions (half as many for pairs)
Finding same collisions in 22.5 milliseconds indicates a high percentage of optimization headroom is used this time, despite having duplicated AABB ids in each cell that have multiple overlapping AABBs.
Grid Implementation With Multi-Threaded Single-AABB Collision Check
Without changing cloud-cloud collision test algorithm, the only optimization left to accelerate the overall collision checking process is multiple-threading. In current state of the sample Grid implementation (out of library header), single-object-AABB collision test is inherently thread-safe as it does not create nor edit any internal state. OpenMP can accelerate this part easily while all-pairs computation requires a custom thread-pool (as in library header).
To test the multi-threaded collision computation (without all-pairs at once but single vs all for N times), following OpenMP parallelization is used (source code):
// a simple global locking point
std::mutex mut;
// fx8150 has 8 integer cores, 4 shared FPUs
#pragma omp parallel for
for(int i=0;i<N;i++)
{
std::vector<AABBofPointCloud<cotype>*> result =
grid.checkCollisionsWithSingleAABB(&AABBs[i]);
for(auto c:result)
{
if(pointCloudIntersection(*c->pCloud,*AABBs[i].pCloud))
{
// modern C++ scope-based locking
std::lock_guard<std::mutex> lg(mut);
collisionMatrix[c->id][AABBs[i].id]=true;
collisionMatrix[AABBs[i].id][c->id]=true;
}
}
}
The output is:
10000 vs 10000 point-clouds collision checking by uniform grid= 13742454 nanoseconds
564 total collisions (half as many for pairs)
13.7 milliseconds, including fine-grain collision check and no special multi-threading optimization (all threads using a global lock instead of non-false-sharing per-element lock ).
Since this performance satisfies the initial performance constraints, tests will continue on harder parts of problem: The Teapot in Stadium.
Third Optimization: Adaptive Grid
Up to this point, the uniform grid has this memory layout:
Where each header is either zero or a positive integer. For the upper sample, if grid is given 6 or more AABB instances to add into same cell's volume, it causes segmentation fault (if that is the last cell in the integer array) or it overwrites other cells' header values and causes undefined behavior.
Even when there is no cell-overflow, a clustering pattern of objects makes big portion of the grid unused due to mostly empty cells between clusters of objects. This forces the uniform grid's settings to have many more AABB capacity per cell and cause a higher time-complexity on top of the latency of allocating a bigger integer buffer.
To reproduce such scenario, the coordinate initialization of objects (point clouds) is given an extra 3 iterations that use very close X, Y, Z center coordinates but too far from center-of-mass of the rest of the clouds (source code):
const int N = 10003;
std::vector<PointCloud<cotype>> objects;
oofrng::Generator<64> gen;
for(int i=0;i<N-3;i++)
{
objects.push_back(PointCloud<cotype>(gen.generate1Float()*450,
gen.generate1Float()*450,gen.generate1Float()*450));
}
// the teapot in stadium problem
objects.push_back(PointCloud<cotype>(10000,10000,10000));
objects.push_back(PointCloud<cotype>(10001,10001,10001));
objects.push_back(PointCloud<cotype>(10002,10002,10002));
and:
// uniform grid for 16x16x16 cells each with 30 objects max
// mapped to (0,0,0) - (10005,10005,10005) cube
// due to the teapot-in-stadium problem, has to have a bigger mapping
Grid<cotype,16,30> grid(0,10005);
The output is:
10003 vs 10003 point-clouds collision checking by uniform grid= 2238980417 nanoseconds
570 total collisions (half as many for pairs)
For only 6 more collisions from 3 objects, the performance dropped to 0.45 FPS (2.2 seconds per computation), with 8 threads in use and 14 seconds for single thread. This is even slower than simple brute-force algorithm.
To optimize memory access pattern, allocation usage and time complexity, each cell is made to adapt incoming number of objects, by only using a different cell-header logic:
On every cell-overflow during insertion, the algorithm adds a new low-resolution low-capacity grid to the parent grid's child-grid (dynamic) array and inserts all the object AABB ids that are in the overflowed cell (and the currently inserted AABB's id) to the new grid, recursively computed until all overflowed AABBs are inserted successfully. To evade infinite recursion, every deeper grid layer is allocated with 2 more AABB capacity per cell.
Same teapot-in-stadium problem is solved using adaptive-grid implementation from header-file of FastCollisionDetectionLib repository (source code):
std::map<int,std::map<int,bool>> collisionMatrix;
{
FastColDetLib::Bench bench(&nano);
// adaptive grid
FastColDetLib::ThreadPool<cotype> thr;
FastColDetLib::AdaptiveGrid<cotype> grid(thr,0,0,0,10005,10005,10005);
// add AABBs to grid
for(int i=0;i<N;i++)
{
grid.add(&AABBs[i],1);
}
std::mutex mut;
#pragma omp parallel for
for(int i=0;i<N;i++)
{
std::vector<FastColDetLib::IParticle<cotype>*> result =
grid.getDynamicCollisionListFor((FastColDetLib::IParticle<cotype>*)&AABBs[i]);
for(auto c:result)
{
if(c->getId() != AABBs[i].getId())
if(pointCloudIntersection(*AABBs[c->getId()].pCloud,*AABBs[i].pCloud))
{
std::lock_guard<std::mutex> lg(mut);
collisionMatrix[c->getId()][AABBs[i].id]=true;
collisionMatrix[AABBs[i].id][c->getId()]=true;
}
}
}
}
The output is as follows:
10003 vs 10003 point-clouds collision checking by uniform grid= 16226199 nanoseconds
570 total collisions (half as many for pairs)
Slightly less than 16.7 milliseconds (60FPS), with 8 threads in-use and simple locking. Adaptation keeps maximum objects per cell low and allocates much lower amount of integer buffer areas that are left unused. Both combine into better caching of (child-grid) traversal and higher density per volume (assuming that the maximum number of same-cell overlapping objects do not reach hundreds on many cells).
Similar performance is shown by multi-threaded all-pairs computation method (source code):
10003 vs 10003 point-clouds collision checking by uniform grid= 16811872 nanoseconds
570 total collisions (half as many for pairs)
FastCollisionDetectionLib's adaptive-grid implementation is only marginally different than this article's contents and is incrementally optimized for more performance (next optimization is multi-threading support for AABB insertion method of grid.add(..) ).
The second part of the challenge was querying collision list for single AABB quicker than 1 microsecond. With a change on the benchmarking:
for(int i=0;i<10003;i++)
{
std::vector<FastColDetLib::IParticle<cotype>*> result;
{
FastColDetLib::Bench bench(&nano);
result = grid.getDynamicCollisionListFor((FastColDetLib::IParticle<cotype>*)&AABBs[i]);
}
std::cout<<1<<" vs "<<N<<" AABB collision checking by adaptive grid=
"<<nano<<" nanoseconds "<<std::endl;
std::cout<<result.size()<<" collisions detected for this AABB"<<std::endl;
}
The output is:
...
1 vs 10003 AABB collision checking by adaptive grid= 1767 nanoseconds
1 collisions detected for this AABB
1 vs 10003 AABB collision checking by adaptive grid= 5340 nanoseconds
1 collisions detected for this AABB
1 vs 10003 AABB collision checking by adaptive grid= 1757 nanoseconds
1 collisions detected for this AABB
1 vs 10003 AABB collision checking by adaptive grid= 1743 nanoseconds
3 collisions detected for this AABB
1 vs 10003 AABB collision checking by adaptive grid= 1276 nanoseconds
3 collisions detected for this AABB
1 vs 10003 AABB collision checking by adaptive grid= 1114 nanoseconds
3 collisions detected for this AABB
It has at least 10% more latency than 1 microsecond given by challenge and only when there are few collisions in a non-branching grid cell. Adaptation has more latency due to grid-to-grid traversing logic.
Latency can be hidden with multithreading or pipelining. With multithreading and no locking (fully independent collision query), 10003 queries finish quicker than a microsecond if per-cell locking is used (less than 16 ms from earlier benchmark):
std::atomic<int> ctr;
ctr.store(0);
{
{
FastColDetLib::Bench bench(&nano);
#pragma omp parallel for
for(int i=0;i<N;i++)
{
std::vector<FastColDetLib::IParticle<cotype>*> result;
result = grid.getDynamicCollisionListFor
((FastColDetLib::IParticle<cotype>*)&AABBs[i]);
ctr+= result.size();
}
}
std::cout<<N<<" vs "<<N<<" AABB collision checking by adaptive grid=
"<<nano<<" nanoseconds "<<std::endl;
std::cout<<"total = "<<ctr.load()<<std::endl;
}
The output is:
10003 vs 10003 AABB collision checking by adaptive grid= 3760629 nanoseconds
total = 10573
3.7 milliseconds for 10k objects is equivalent to 370 nanoseconds per object.
The FastColDetLib library works only on pointers of IParticle interface (and decouples the user-implementation from library implementation) to maintain different types of objects within same scene. Interface expects user to implement these methods:
struct AABBofPointCloud: public FastColDetLib::IParticle<CoordType>
{
...
const CoordType getMaxX()const {return xmax;}
const CoordType getMaxY()const {return ymax;}
const CoordType getMaxZ()const {return zmax;}
const CoordType getMinX()const {return xmin;}
const CoordType getMinY()const {return ymin;}
const CoordType getMinZ()const {return zmin;}
const int getId()const {return id;}
...
};
getMaxX/Y/Z and getMinX/Y/Z methods are used for computing collisions while getId method is used to evade duplications inside all-pairs computation (grid.getCollisions()). Working only with pointers makes algorithm use less temporary memory but adds an indirection overhead. This indirection overhead can be partially hidden by use of threads.
All-Pairs Collision Test For 20k AABBs at 60 FPS
The second challenge to reach 60 FPS for all-pairs collision detection with 20k AABBs requires a complete re-write of adaptive grid codes due to multiple reasons:
- Tree-like structures (such as adaptive grid) have pointer-chasing between nodes. Chasing pointers is slower than traversing a linear array by being less cache-friendly.
- Each node of tree is an actual object and means an allocation per instance. Allocations are slow and possibly serialized by OS to do book-keeping during memory fragmentation.
- Each node contains a lot of particle data, there is no data re-use between nodes. This is not cache-friendly (causes high cache-miss ratio).
- AABB-AABB collision pair computations do not use data-locality and run on non-contiguous data that is much less cache-friendly and non-vectorizable for SIMD units of CPU cores.
- Node-AABB collision tests are not evaded (the collision mask is currently an array of integers) by early-quitting
- Tree structure is dense and creates all of the child nodes per parent node that leads to worse cache-miss ratio.
- Computation is in array of structs (AOS) pattern which leads to less cache-line efficiency
Solutions:
- Pointer-chasing causing less caching --> implement a linear tree on a buffer
- Too many allocations (per node) --> use a memory pool
- Too many object fields per node --> separate the fields from node
- Non contiguous + non-local data access --> do tiled computing on simple arrays and let the compiler do the vectorization
- No early-quit in node<-->AABB collision check: use bitmap as collision mask (4x4x4 = 64 bits per node)
- Unused nodes: implement a sparse tree that does not allocate empty child nodes
All of above solutions overlap on a data structure: sparse linear adaptive-grid backed by memory-pool (with tiled collision computing)
Sparse Linear Adaptive Grid Implementation
To serve the linear-tree implementation with high-throughput pseudo-allocations, a memory-pool is needed first (found in same implementation header file).
Memory Pool
For current project, memory pool implementation is developed with repeated reset --> allocate --> reset --> allocate chained-use in mind. It's purpose is to do allocations only when internal capacity is overflowed and return from all allocation method calls quickly, to let collision-checking algorithm have stability in terms of latency and memory consumption.
To have memory consumption stability, it does real-allocation only with integer-powers-of-2 which does increase in steps of 1024 elements, 2k elements, 4k elements, 8k elements until allocation size criteria is reached. Once 1 million elements are real-allocated, it does quick-return from any less-than-1M-element allocation after single reset. Exponential growth of memory allocation minimizes number of real-allocations and maintains stability only after few iterations of collision detection loop.
Implementation has basic data access methods of get and set, features a reset method to revert all allocations with O(1) complexity and an allocation method that frequently completes in O(1) complexity:
template<typename DataType>
class Memory
{
public:
Memory()
{
memory=std::make_shared<std::vector<DataType>>();
allocPtr=std::make_shared<int>();
*allocPtr = 0;
allocPtrPtr=allocPtr.get();
memory->resize(1024);
ptr=memory->data();
}
inline
DataType * getPtr(const int index) const noexcept
{
return ptr+index;
}
inline
DataType& getRef(const int index) const noexcept
{
return ((DataType* __restrict__ const)ptr)[index];
}
inline
const DataType get(const int index) const noexcept
{
return ((DataType* __restrict__ const)ptr)[index];
}
inline
void set(const int index, const DataType data) const noexcept
{
((DataType* __restrict__ const)ptr)[index]=data;
}
inline
void readFrom(Memory<DataType>& mem, const int index, const int indexThis, const int n)
{
std::copy(mem.ptr+index,mem.ptr+index+n,ptr+indexThis);
}
inline
void writeTo(std::vector<DataType>& vec)
{
std::copy(ptr,ptr+*allocPtrPtr,vec.data());
}
inline
const int allocate(const int size)
{
const int result = *allocPtrPtr;
while(size + *allocPtrPtr >= memory->size())
{
memory->resize(memory->size()*2);
}
*allocPtrPtr += size;
ptr=memory->data();
return result;
}
inline
const int capacity()
{
return memory->size();
}
inline
const int size()
{
return *allocPtrPtr;
}
inline
void reset()
{
*allocPtrPtr = 0;
}
private:
DataType* ptr;
std::shared_ptr<int> allocPtr;
int* allocPtrPtr;
std::shared_ptr<std::vector<DataType>> memory;
};
struct MemoryPool
{
void clear()
{
nodeCollisionMask.reset();
childNodeCount.reset();
index.reset();
indexParticle.reset();
orderParticle.reset();
minX.reset();
maxX.reset();
minY.reset();
maxY.reset();
minZ.reset();
maxZ.reset();
nodeMinX.reset();
nodeMinY.reset();
nodeMinZ.reset();
nodeInvWidth.reset();
nodeInvHeight.reset();
nodeInvDepth.reset();
}
// node-particle collision
Memory<uint64_t> nodeCollisionMask;
Memory<char> childNodeCount;
Memory<int> index;
Memory<int> indexParticle;
Memory<int> orderParticle;
Memory<float> nodeMinX;
Memory<float> nodeMinY;
Memory<float> nodeMinZ;
Memory<float> nodeInvWidth;
Memory<float> nodeInvHeight;
Memory<float> nodeInvDepth;
Memory<float> minX;
Memory<float> maxX;
Memory<float> minY;
Memory<float> maxY;
Memory<float> minZ;
Memory<float> maxZ;
Memory<int> idTmp[64];
Memory<int> orderTmp[64];
Memory<std::pair<int,int>> allPairsColl;
Memory<FastUnique<int32_t, testParticleLimit>> allPairsCollmapping;
};
Compared to an std::vector, this class optimizes memory consumption by keeping only a single-internal-data for all clones of same instance and features less number of allocations with relatively cheap allocation and clear(reset) methods.
For non-linear data structures with unknown construction patterns, memory pool must have a complex allocation-control logic rather than this simple implementation. For a linear adaptive grid, this is enough to serve all allocations, fast.
Performance test for the Memory component on an array of integers:
FastColDetLib::Memory<int> mem;
size_t measure;
for(int j=0;j<15;j++)
{
FastColDetLib::Bench bench(&measure);
mem.reset();
for(int i=0;i<100000+j*200000;i++)
{
int index = mem.allocate(3);
mem.set(index,0);
mem.set(index+1,1);
mem.set(index+2,2);
}
std::cout<<"Memory (size="<<100000+j*200000<<"): "<<measure<<" ns"<<std::endl;
}
std::vector<int> mem2;
for(int j=0;j<15;j++)
{
FastColDetLib::Bench bench(&measure);
mem2.clear();
for(int i=0;i<100000+j*200000;i++)
{
mem2.push_back(0);
mem2.push_back(1);
mem2.push_back(2);
}
std::cout<<"Vector (size="<<100000+j*200000<<"): "<<measure<<" ns"<<std::endl;
}
Both std::vector and Memory instances are tested for their on-demand allocation(unknown memory requirements) and single-allocation(known memory requirements):
Memory (size=100000): 94674792711856 ns // cold benchmark start = low performance
Memory (size=300000): 6486661 ns
Memory (size=500000): 11162508 ns
Memory (size=700000): 22083055 ns
Memory (size=900000): 42743681 ns
Memory (size=1100000): 6999557 ns
Memory (size=1300000): 8683617 ns
Memory (size=1500000): 10757706 ns
Memory (size=1700000): 83456551 ns
Memory (size=1900000): 14201669 ns
Memory (size=2100000): 16036462 ns
Memory (size=2300000): 17733826 ns
Memory (size=2500000): 18858536 ns
Memory (size=2700000): 20413091 ns
Memory (size=2900000): 23847971 ns
Vector (size=100000): 159671661 ns
Vector (size=300000): 4493545 ns
Vector (size=500000): 10269529 ns
Vector (size=700000): 19388296 ns
Vector (size=900000): 34455068 ns
Vector (size=1100000): 11864543 ns
Vector (size=1300000): 14701698 ns
Vector (size=1500000): 16956325 ns
Vector (size=1700000): 71052797 ns
Vector (size=1900000): 21863594 ns
Vector (size=2100000): 23666274 ns
Vector (size=2300000): 26714740 ns
Vector (size=2500000): 28240470 ns
Vector (size=2700000): 31571745 ns
Vector (size=2900000): 32961081 ns
After Memory instance real-allocates in first few benchmark iterations, following tests nearly always run on non-allocation code paths and gain 10%-50% more performance than std::vector under unknown memory requirements with gradually increasing total-allocation sizes.
When allocation size is known, both are equal (resize + [ ] operator for vector, allocating once for Memory) in performance.
Internal Fields Of Linear Sparse Adaptive Grid
Due to MemoryPool being used for all nodes' data, the grid object itself needs to maintain only root node's spatial properties:
- bounding box corners of root node: minCornerX/Y/Z and maxCornerX/Y/Z
- cell sizes of root node: cellWidth/Height/Depth
- inverse cell sizes to reduce number of integer division operations: cellWidthInv/HeightInv/DepthInv
struct AdaptiveGridV2Fields
{
AdaptiveGridV2Fields(MemoryPool mPool, const float minx, const float miny, const float minz,
const float maxx, const float maxy, const float maxz):mem(mPool),
minCornerX(minx),minCornerY(miny),minCornerZ(minz),maxCornerX(maxx),maxCornerY(maxy),maxCornerZ(maxz),
cellWidth ((maxx-minx)*0.25f),
cellHeight ((maxy-miny)*0.25f),
cellDepth ((maxz-minz)*0.25f),
cellWidthInv (1.0f/((maxx-minx)*0.25f)),
cellHeightInv(1.0f/((maxy-miny)*0.25f)),
cellDepthInv (1.0f/((maxz-minz)*0.25f))
{
}
MemoryPool mem;
const float minCornerX;
const float minCornerY;
const float minCornerZ;
const float maxCornerX;
const float maxCornerY;
const float maxCornerZ;
const float cellWidth;
const float cellHeight;
const float cellDepth;
const float cellWidthInv;
const float cellHeightInv;
const float cellDepthInv;
};
This struct is used as main internal data of class AdaptiveGridV2 that has its name indicating optimizations for the challenge-2 (20k AABB all-pairs compute in 16.7 ms).
class AdaptiveGridV2
{
public:
// constructs adaptive grid for a given AABB volume
AdaptiveGridV2(MemoryPool mem,
const float minx, const float miny, const float minz,
const float maxx, const float maxy, const float maxz);
// clears memory pool, to be reused later (for rebuilding the tree)
void clear();
template<typename Derived>
inline void addParticles(const int numParticlesToAdd,
Derived * const __restrict__ particles)
{ .. adds AABBs to grid using IParticle<float> interface of Derived class .. }
// test collisions with an AABB, returns vector of id values of colliding AABBs
std::vector<int> findCollisions(const float minx, const float miny,
const float minz, const float maxx,
const float maxy, const float maxz);
// test all collisions between all AABBs inside grid
std::vector<std::pair<int,int>> findCollisionsAll();
void buildTree();
private:
std::shared_ptr<AdaptiveGridV2Fields> fields; // single shared data
}
This lets any instance to be copied or moved without any accidental-copying while saving readability.
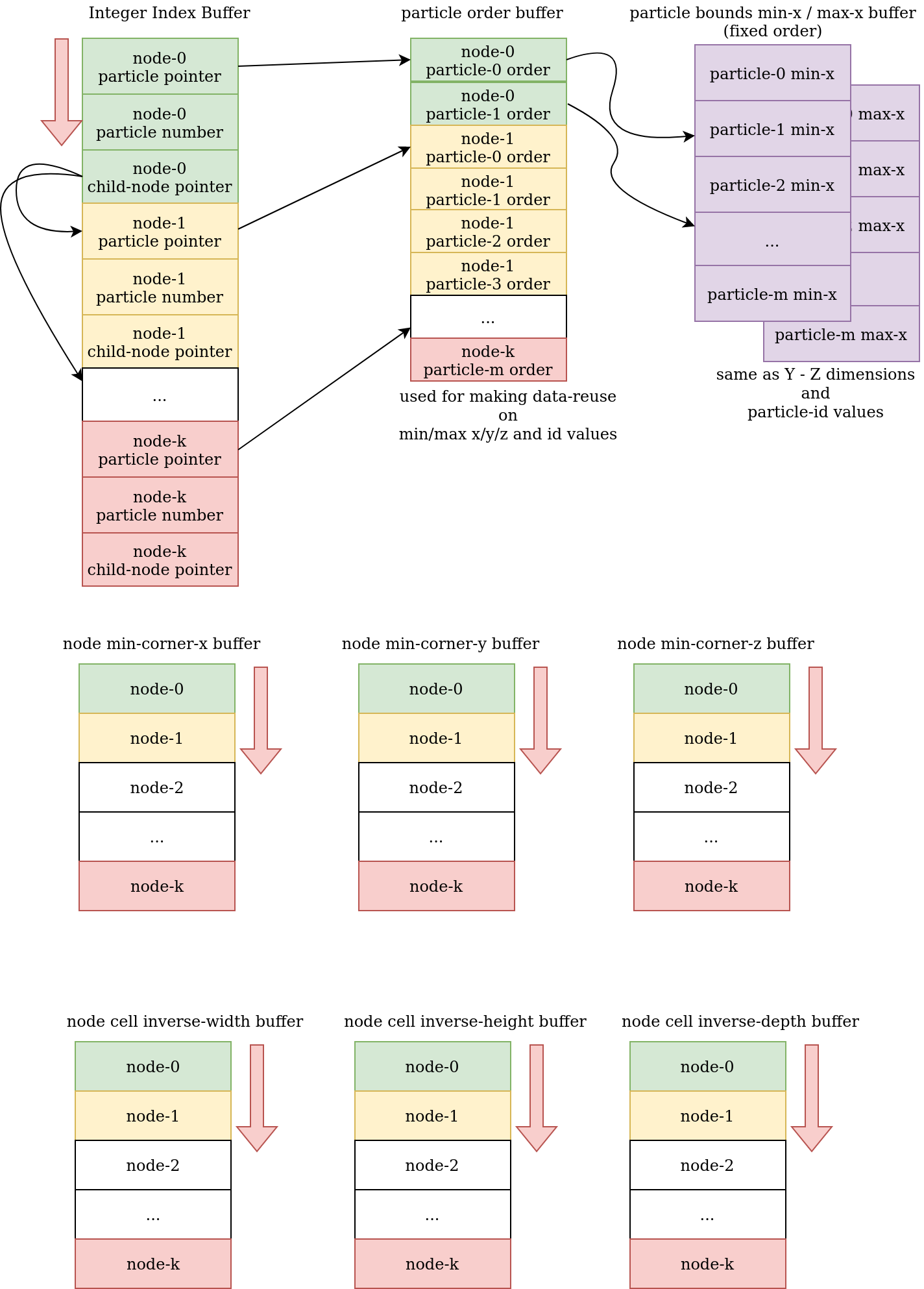
Tree Node Representation On Buffer
With new data representation, there is no real object for any node other than root node. The node contains three main integer fields for particle-list pointer, particle list size and child-node pointer. These three fields are found contigously on same integer buffer while side-fields (min-corner x/y/z and inverse cell size x/y/z) are saved on 6 different float-type buffers.
Adding Particles Into Root
Original particle data is inserted only to root and building the tree only takes references (order value) from the particle buffer of root when creating child nodes.
Adding particles:
template<typename Derived>
inline void addParticles(const int numParticlesToAdd, Derived * const __restrict__ particles)
{
const int pId = fields->mem.indexParticle.allocate(numParticlesToAdd);
const int oId = fields->mem.orderParticle.allocate(numParticlesToAdd);
const int maxXId = fields->mem.maxX.allocate(numParticlesToAdd);
const int maxYId = fields->mem.maxY.allocate(numParticlesToAdd);
const int maxZId = fields->mem.maxZ.allocate(numParticlesToAdd);
const int minXId = fields->mem.minX.allocate(numParticlesToAdd);
const int minYId = fields->mem.minY.allocate(numParticlesToAdd);
const int minZId = fields->mem.minZ.allocate(numParticlesToAdd);
fields->mem.index.set(1,fields->mem.index.get(1)+numParticlesToAdd);
for(int i=0;i<numParticlesToAdd;i++)
{
const IParticle<float> * const curPtr = static_cast<const IParticle<float>* const>(particles+i);
fields->mem.indexParticle.set(pId+i,curPtr->getId());
fields->mem.orderParticle.set(oId+i,oId+i);
fields->mem.maxX.set(maxXId+i,curPtr->getMaxX());
fields->mem.maxY.set(maxYId+i,curPtr->getMaxY());
fields->mem.maxZ.set(maxZId+i,curPtr->getMaxZ());
fields->mem.minX.set(minXId+i,curPtr->getMinX());
fields->mem.minY.set(minYId+i,curPtr->getMinY());
fields->mem.minZ.set(minZId+i,curPtr->getMinZ());
}
}
When particles are added in large chunks (n>1), insertion operation for 20000 randomly placed particles takes close to a millisecond on system of 2.1GHz Fx8150 and 1 channel 1333MHz ddr3 memory.
Tree Building Procedure
Building the linear (or serialized) representation of the adaptive grid's tree is straightforward. Pseudo-codes for basic workflow is given below:
current = root
last item = root + 3 [3=node size in number of integers]
while current offset < last item offset
if current has more particles than 32
this is now an internal node
map particles to 1-64 child nodes (create child nodes sparsely)
for each created child node
compute bitmask (uint64_t) for early quitting from collision computation
(4x4x4 = uint64_t, 2x2x2 = uint8_t, 1 bit per child node position)
copy the mapped particle-id values to child node
last item = child node
else
this is now a leaf node
number of child nodes = 0
save offset to leaf-list (for fast-traversing all leaves in all-pairs detection)
following is the implementation:
void buildTree()
{
int particleStart = fields->mem.index.get(0);
int numParticle = fields->mem.index.get(1);
int nodeOffset = 0;
float minCornerX = fields->mem.nodeMinX.get(0);
float minCornerY = fields->mem.nodeMinY.get(0);
float minCornerZ = fields->mem.nodeMinZ.get(0);
float cellWidthInv = fields->mem.nodeInvWidth.get(0);
float cellHeightInv = fields->mem.nodeInvHeight.get(0);
float cellDepthInv = fields->mem.nodeInvDepth.get(0);
float cellWidth = 1.0f/cellWidthInv;
float cellHeight = 1.0f/cellHeightInv;
float cellDepth = 1.0f/cellDepthInv;
int ctr=0;
int maxNodeOffset = 3;
while(nodeOffset <= maxNodeOffset)
{
ctr++;
int ctrTmp[64]={0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0,
0,0,0,0,0,0,0,0};
// if child node pointer not set up
if(fields->mem.index.get(nodeOffset+2)<nodeOffset && fields->mem.index.get(fields->mem.index.get(nodeOffset+2)+2)>=0)
{
fields->mem.index.set(fields->mem.index.get(nodeOffset+2)+2,-(nodeOffset+1));
}
int childNodeCount = 0;
if(numParticle > testParticleLimit)
{
{
for(int zz = 0; zz<4; zz++)
for(int yy = 0; yy<4; yy++)
for(int xx = 0; xx<4; xx++)
{
// allocate node
const int index0 = xx+yy*4+zz*16;
fields->mem.orderTmp[index0].reset();
fields->mem.orderTmp[index0].allocate(numParticle);
}
}
{
for(int ii=0;ii<numParticle;ii++)
{
const int orderParticle = fields->mem.orderParticle.get(particleStart+ii);
const float& minx = fields->mem.minX.getRef(orderParticle);
const float& miny = fields->mem.minY.getRef(orderParticle);
const float& minz = fields->mem.minZ.getRef(orderParticle);
const float& maxx = fields->mem.maxX.getRef(orderParticle);
const float& maxy = fields->mem.maxY.getRef(orderParticle);
const float& maxz = fields->mem.maxZ.getRef(orderParticle);
const int indexStartX = std::floor((minx - minCornerX)*cellWidthInv);
const int indexEndX = std::floor((maxx - minCornerX)*cellWidthInv);
const int indexStartY = std::floor((miny - minCornerY)*cellHeightInv);
const int indexEndY = std::floor((maxy - minCornerY)*cellHeightInv);
const int indexStartZ = std::floor((minz -minCornerZ)*cellDepthInv);
const int indexEndZ = std::floor((maxz - minCornerZ)*cellDepthInv);
// prepare cell indicator mask (1 bit = has object, 0 bit = empty))
for(int k=indexStartZ; k<=indexEndZ; k++)
{
if(k<0 || k>=4)
continue;
for(int j=indexStartY; j<=indexEndY; j++)
{
if(j<0 || j>=4)
continue;
for(int i=indexStartX; i<=indexEndX; i++)
{
if(i<0 || i>=4)
continue;
const int index0 = i+j*4+k*16;
fields->mem.orderTmp[index0].set(ctrTmp[index0],orderParticle);
ctrTmp[index0]++;
}
}
}
}
}
// add all particles in order (from first child node to last child node)
childNodeCount=0;
for(int zz = 0; zz<4; zz++)
for(int yy = 0; yy<4; yy++)
for(int xx = 0; xx<4; xx++)
{
const int index0 = xx+yy*4+zz*16;
const int sz = ctrTmp[index0];
if(sz>0)
{
childNodeCount++;
const int nodeIndexOfs = fields->mem.index.allocate(3);
const int particleStartCur = nodeIndexOfs;
const int numParticleCur = nodeIndexOfs+1;
const int childNodeStartCur = nodeIndexOfs+2;
const int tmpIndex = fields->mem.childNodeCount.allocate(1);
const int nodeBoundMinXFloat = fields->mem.nodeMinX.allocate(1);
const int nodeBoundMinYFloat = fields->mem.nodeMinY.allocate(1);
const int nodeBoundMinZFloat = fields->mem.nodeMinZ.allocate(1);
const int nodeInvWidthFloat = fields->mem.nodeInvWidth.allocate(1);
const int nodeInvHeightFloat = fields->mem.nodeInvHeight.allocate(1);
const int nodeInvDepthFloat = fields->mem.nodeInvDepth.allocate(1);
fields->mem.nodeMinX.set(nodeBoundMinXFloat,minCornerX+xx*cellWidth);
fields->mem.nodeMinY.set(nodeBoundMinYFloat,minCornerY+yy*cellHeight);
fields->mem.nodeMinZ.set(nodeBoundMinZFloat,minCornerZ+zz*cellDepth);
fields->mem.nodeInvWidth.set(nodeInvWidthFloat,cellWidthInv*4.0f);
fields->mem.nodeInvHeight.set(nodeInvHeightFloat,cellHeightInv*4.0f);
fields->mem.nodeInvDepth.set(nodeInvDepthFloat,cellDepthInv*4.0f);
const int nodeMaskIndex = fields->mem.nodeCollisionMask.allocate(1);
uint64_t nodeMask = 0;
storeBit(nodeMask,1,index0);
fields->mem.nodeCollisionMask.set(nodeMaskIndex,nodeMask);
const int allocOffset = fields->mem.orderParticle.allocate(sz);
fields->mem.orderParticle.readFrom(fields->mem.orderTmp[index0],0,allocOffset,sz);
fields->mem.index.set(particleStartCur,allocOffset);
fields->mem.index.set(numParticleCur,sz);
fields->mem.index.set(childNodeStartCur,nodeOffset);
maxNodeOffset=particleStartCur;
}
}
fields->mem.childNodeCount.set(nodeOffset/3,childNodeCount);
}
else
{
fields->mem.childNodeCount.set(nodeOffset/3,0);
const int idx = fields->mem.leafOffset.allocate(1);
fields->mem.leafOffset.set(idx,nodeOffset);
}
nodeOffset += 3;
numParticle=0;
if(nodeOffset <= maxNodeOffset)
{
particleStart = fields->mem.index.get(nodeOffset);
numParticle = fields->mem.index.get(nodeOffset+1);
minCornerX = fields->mem.nodeMinX.get(nodeOffset/3);
minCornerY = fields->mem.nodeMinY.get(nodeOffset/3);
minCornerZ = fields->mem.nodeMinZ.get(nodeOffset/3);
cellWidthInv = fields->mem.nodeInvWidth.get(nodeOffset/3);
cellHeightInv = fields->mem.nodeInvHeight.get(nodeOffset/3);
cellDepthInv = fields->mem.nodeInvDepth.get(nodeOffset/3);
cellWidth = 1.0f/cellWidthInv;
cellHeight = 1.0f/cellHeightInv;
cellDepth = 1.0f/cellDepthInv;
}
}
}
Due to the serialized form and extra bookkeeping to compute child-node offset values by backtracking, it looks more complex than it is.
Benchmark timings for tree-building + particle insertion:
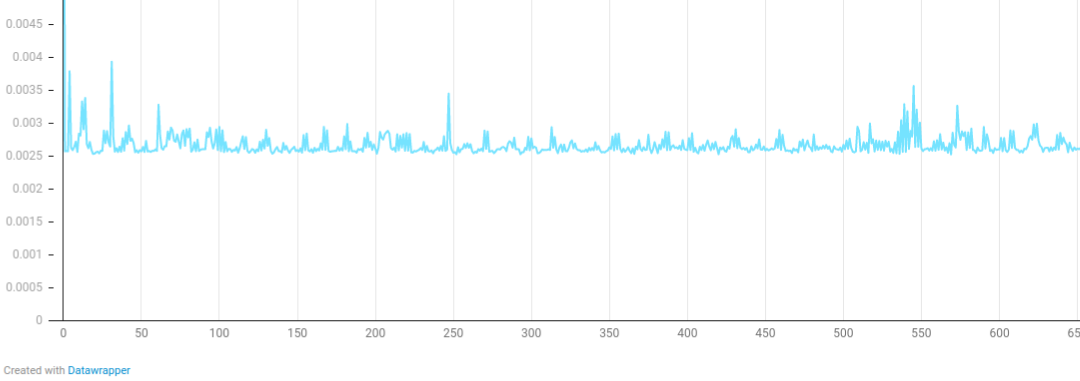
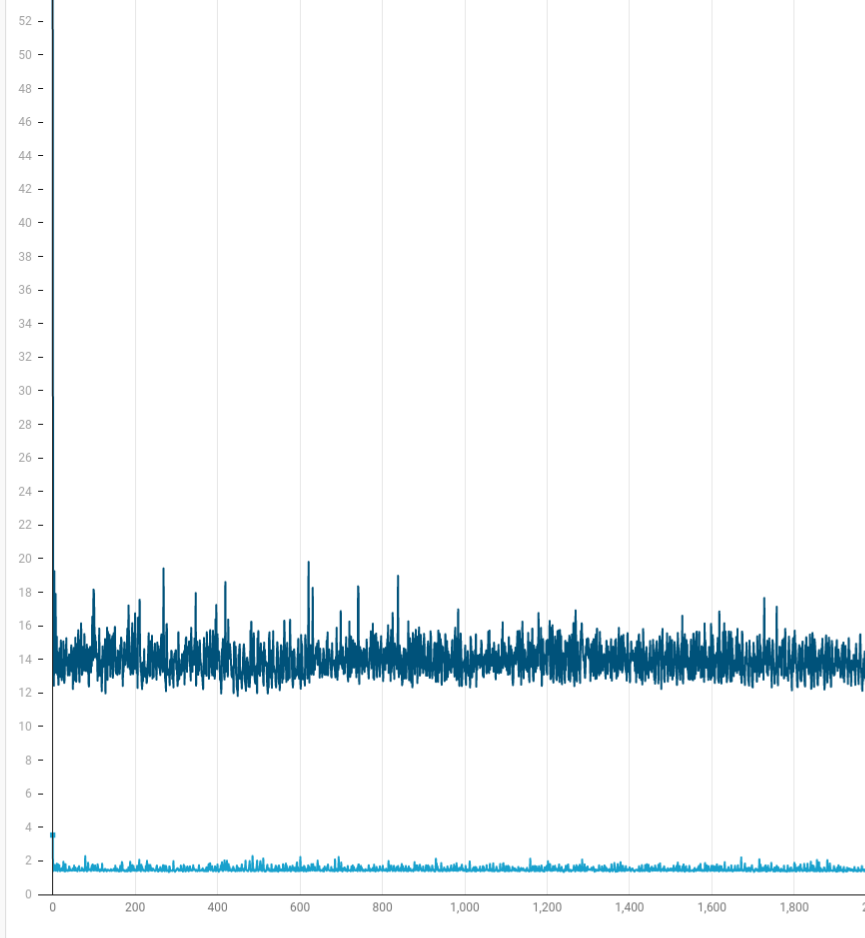
Random starting positions and randomly moving, 0 collisions, 20000 particles for 650 timesteps
Y-axis: seconds (initial allocations cause peaks up to 6.75 milliseconds)
X-axis: time step (up to 650th)
Crystalline pattern starting positions and no movement, 0 collisions, 20000 particles
Y-axis: seconds
X-axis: time step
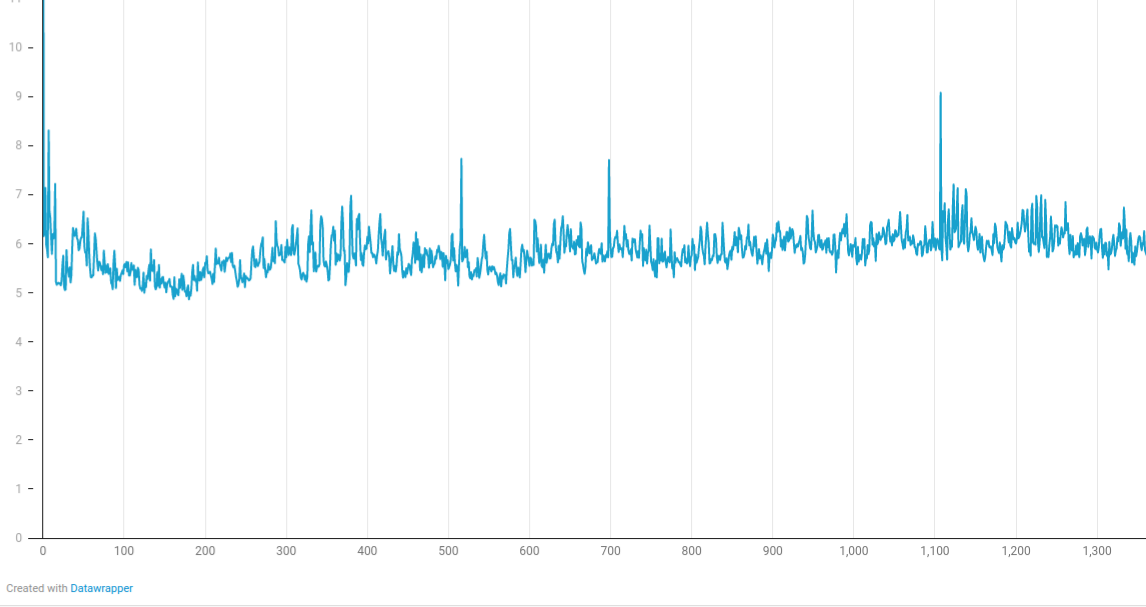
Random start, random movement, 20000 particles, 10000+ collisions each timestep
Y-axis: milliseconds
X-axis: time step
Collisions: start with 15000, rapidly approach 9000 then gradually increase to 14000.
In random-collision sample with more than half of particles overlapping another particle, tree-build time increases due to increased number of internal tree nodes. On every few hundred timesteps, the build time reaches 9 milliseconds due to sub-optimal tree balance on number of particles versus tree depth. This leaves ~7.7 milliseconds headroom to compute the all-pairs collision.
To keep run-time of all-pair computations low enough, the implementation limits number of particles per leaf node to 32 and computes each leaf as brute-force using implicitly vectorized code pattern (to be compatible with future processors such as Cascadelake of Intel (please see benchmark results below for AVX512 efficiency)).
All-Pairs Collision Check
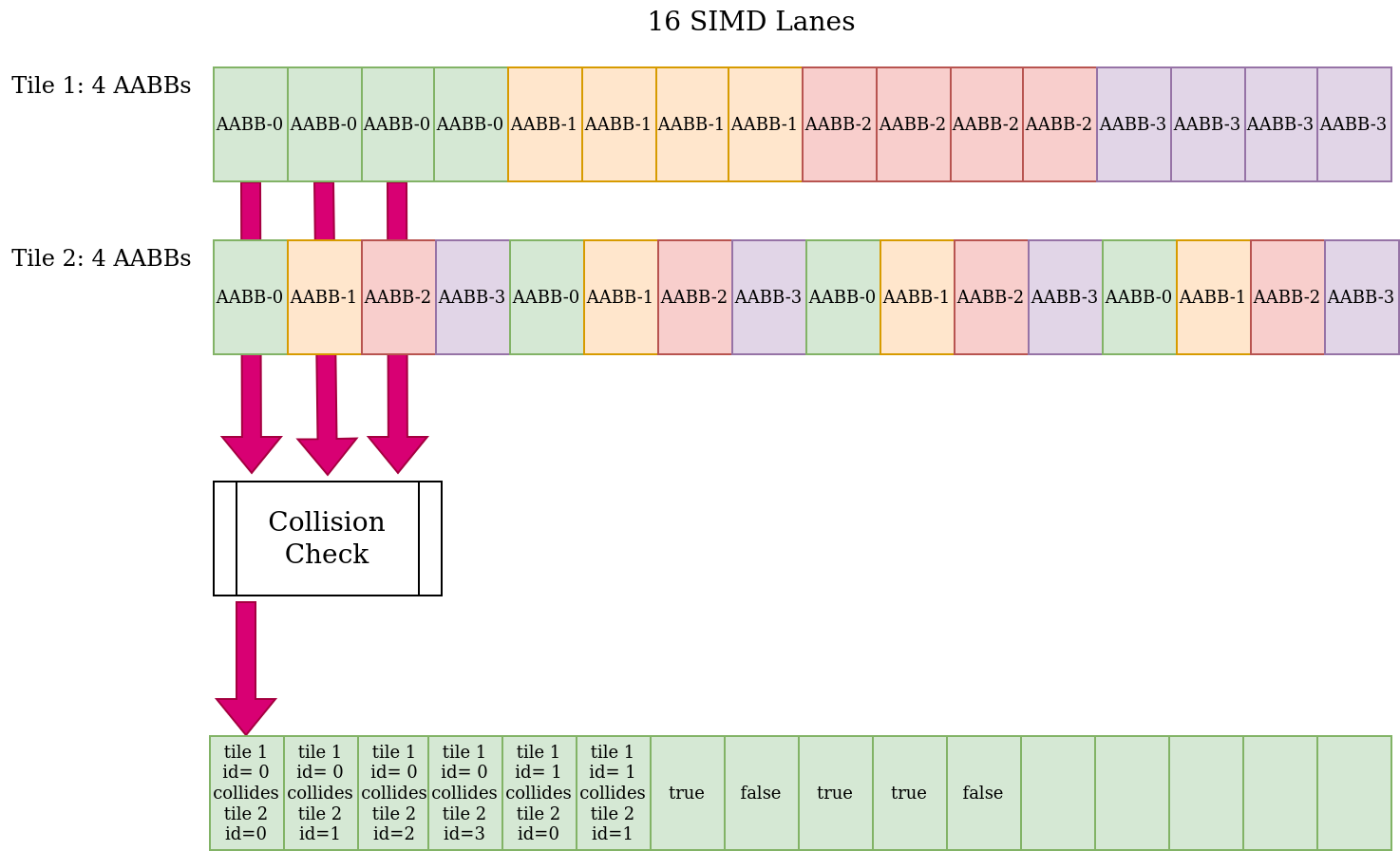
Since the particle data is not stored linearly for each leaf node (it was in first challenge) but referenced to orginal particle buffer of root node, a temporary linear storage is required to let compiler vectorize the computations. First, the region of computation (up to 32 particles within each leaf node) is copied to arrays on stack, in struct-of-arrays manner (id values have their own buffer, coordinates have their own buffer). Second, the compute region is divided into smaller chunks (of 4-length each). Lastly, each chunk of 4 elements is compared against all other chunks of 4 elements (except the chunks that make duplicated work). This makes 1 chunk vs chunk comparison for only 4 particles, 2 chunk vs chunk comparisons for 8 particles, 6 chunk vs chunk comparisons for 12 particles, up to 28 chunk comparisons for 32 particles.
Each chunk versus chunk comparison is made by simple ordered operations within their own loops to help compiler find an easy solution for vectorization. It is similar to how CUDA/OpenCL kernels running on warps/wavefronts in lock-step manner, only with difference of 16-wide SIMD support here.
Collision check first does id comparison to mask (in each vectorized chunk) duplicated work within each SIMD operation (and to reduce work required after vectorized computation). Then it does "AND" operation for each coordinate of AABBs to find result per pair. Since all operations are made on 16-wide vectors, the computations can map well enough to any instruction set from MMX to AVX512.
4x4 Elements Chunk Comparison Function
inline
const int intersectDim(const float minx, const float maxx, const float minx2, const float maxx2) noexcept
{
return !((maxx < minx2) || (maxx2 < minx));
}
void comp4vs4( const int * const __restrict__ partId1, const int * const __restrict__ partId2,
const float * const __restrict__ minx1, const float * const __restrict__ minx2,
const float * const __restrict__ miny1, const float * const __restrict__ miny2,
const float * const __restrict__ minz1, const float * const __restrict__ minz2,
const float * const __restrict__ maxx1, const float * const __restrict__ maxx2,
const float * const __restrict__ maxy1, const float * const __restrict__ maxy2,
const float * const __restrict__ maxz1, const float * const __restrict__ maxz2,
int * const __restrict__ out
)
{
alignas(32)
int result[16]={
// 0v0 0v1 0v2 0v3
// 1v0 1v1 1v2 1v3
// 2v0 2v1 2v2 2v3
// 3v0 3v1 3v2 3v3
0, 0, 0, 0,
0, 0, 0, 0,
0, 0, 0, 0,
0, 0, 0, 0
};
alignas(32)
int tileId1[16]={
// 0,1,2,3,0,1,2,3,0,1,2,3,0,1,2,3
partId1[0],partId1[1],partId1[2],partId1[3],
partId1[0],partId1[1],partId1[2],partId1[3],
partId1[0],partId1[1],partId1[2],partId1[3],
partId1[0],partId1[1],partId1[2],partId1[3]
};
alignas(32)
int tileId2[16]={
// 0,0,0,0,1,1,1,1,2,2,2,2,3,3,3,3
partId2[0],partId2[0],partId2[0],partId2[0],
partId2[1],partId2[1],partId2[1],partId2[1],
partId2[2],partId2[2],partId2[2],partId2[2],
partId2[3],partId2[3],partId2[3],partId2[3]
};
alignas(32)
float tileMinX1[16]={
// 0,1,2,3,0,1,2,3,0,1,2,3,0,1,2,3
minx1[0],minx1[1],minx1[2],minx1[3],
minx1[0],minx1[1],minx1[2],minx1[3],
minx1[0],minx1[1],minx1[2],minx1[3],
minx1[0],minx1[1],minx1[2],minx1[3]
};
alignas(32)
float tileMinX2[16]={
// 0,0,0,0,1,1,1,1,2,2,2,2,3,3,3,3
minx2[0],minx2[0],minx2[0],minx2[0],
minx2[1],minx2[1],minx2[1],minx2[1],
minx2[2],minx2[2],minx2[2],minx2[2],
minx2[3],minx2[3],minx2[3],minx2[3]
};
alignas(32)
float tileMinY1[16]={
// 0,1,2,3,0,1,2,3,0,1,2,3,0,1,2,3
miny1[0],miny1[1],miny1[2],miny1[3],
miny1[0],miny1[1],miny1[2],miny1[3],
miny1[0],miny1[1],miny1[2],miny1[3],
miny1[0],miny1[1],miny1[2],miny1[3]
};
alignas(32)
float tileMinY2[16]={
// 0,0,0,0,1,1,1,1,2,2,2,2,3,3,3,3
miny2[0],miny2[0],miny2[0],miny2[0],
miny2[1],miny2[1],miny2[1],miny2[1],
miny2[2],miny2[2],miny2[2],miny2[2],
miny2[3],miny2[3],miny2[3],miny2[3]
};
alignas(32)
float tileMinZ1[16]={
// 0,1,2,3,0,1,2,3,0,1,2,3,0,1,2,3
minz1[0],minz1[1],minz1[2],minz1[3],
minz1[0],minz1[1],minz1[2],minz1[3],
minz1[0],minz1[1],minz1[2],minz1[3],
minz1[0],minz1[1],minz1[2],minz1[3]
};
alignas(32)
float tileMinZ2[16]={
// 0,0,0,0,1,1,1,1,2,2,2,2,3,3,3,3
minz2[0],minz2[0],minz2[0],minz2[0],
minz2[1],minz2[1],minz2[1],minz2[1],
minz2[2],minz2[2],minz2[2],minz2[2],
minz2[3],minz2[3],minz2[3],minz2[3]
};
alignas(32)
float tileMaxX1[16]={
// 0,1,2,3,0,1,2,3,0,1,2,3,0,1,2,3
maxx1[0],maxx1[1],maxx1[2],maxx1[3],
maxx1[0],maxx1[1],maxx1[2],maxx1[3],
maxx1[0],maxx1[1],maxx1[2],maxx1[3],
maxx1[0],maxx1[1],maxx1[2],maxx1[3]
};
alignas(32)
float tileMaxX2[16]={
// 0,0,0,0,1,1,1,1,2,2,2,2,3,3,3,3
maxx2[0],maxx2[0],maxx2[0],maxx2[0],
maxx2[1],maxx2[1],maxx2[1],maxx2[1],
maxx2[2],maxx2[2],maxx2[2],maxx2[2],
maxx2[3],maxx2[3],maxx2[3],maxx2[3]
};
alignas(32)
float tileMaxY1[16]={
// 0,1,2,3,0,1,2,3,0,1,2,3,0,1,2,3
maxy1[0],maxy1[1],maxy1[2],maxy1[3],
maxy1[0],maxy1[1],maxy1[2],maxy1[3],
maxy1[0],maxy1[1],maxy1[2],maxy1[3],
maxy1[0],maxy1[1],maxy1[2],maxy1[3]
};
alignas(32)
float tileMaxY2[16]={
// 0,0,0,0,1,1,1,1,2,2,2,2,3,3,3,3
maxy2[0],maxy2[0],maxy2[0],maxy2[0],
maxy2[1],maxy2[1],maxy2[1],maxy2[1],
maxy2[2],maxy2[2],maxy2[2],maxy2[2],
maxy2[3],maxy2[3],maxy2[3],maxy2[3]
};
alignas(32)
float tileMaxZ1[16]={
// 0,1,2,3,0,1,2,3,0,1,2,3,0,1,2,3
maxz1[0],maxz1[1],maxz1[2],maxz1[3],
maxz1[0],maxz1[1],maxz1[2],maxz1[3],
maxz1[0],maxz1[1],maxz1[2],maxz1[3],
maxz1[0],maxz1[1],maxz1[2],maxz1[3]
};
alignas(32)
float tileMaxZ2[16]={
// 0,0,0,0,1,1,1,1,2,2,2,2,3,3,3,3
maxz2[0],maxz2[0],maxz2[0],maxz2[0],
maxz2[1],maxz2[1],maxz2[1],maxz2[1],
maxz2[2],maxz2[2],maxz2[2],maxz2[2],
maxz2[3],maxz2[3],maxz2[3],maxz2[3]
};
for(int i=0;i<16;i++)
result[i] = (tileId1[i] < tileId2[i]);
for(int i=0;i<16;i++)
result[i] = result[i] &&
intersectDim(tileMinX1[i], tileMaxX1[i], tileMinX2[i], tileMaxX2[i]) &&
intersectDim(tileMinY1[i], tileMaxY1[i], tileMinY2[i], tileMaxY2[i]) &&
intersectDim(tileMinZ1[i], tileMaxZ1[i], tileMinZ2[i], tileMaxZ2[i]);
for(int i=0;i<16;i++)
out[i]=result[i];
};
After initializing input arrays for both tiles, it takes only two loops to compute 16 different comparisons, possibly using only several CPU instructions in case of AVX512. According to godbolt.org, also the initialization is vectorized:
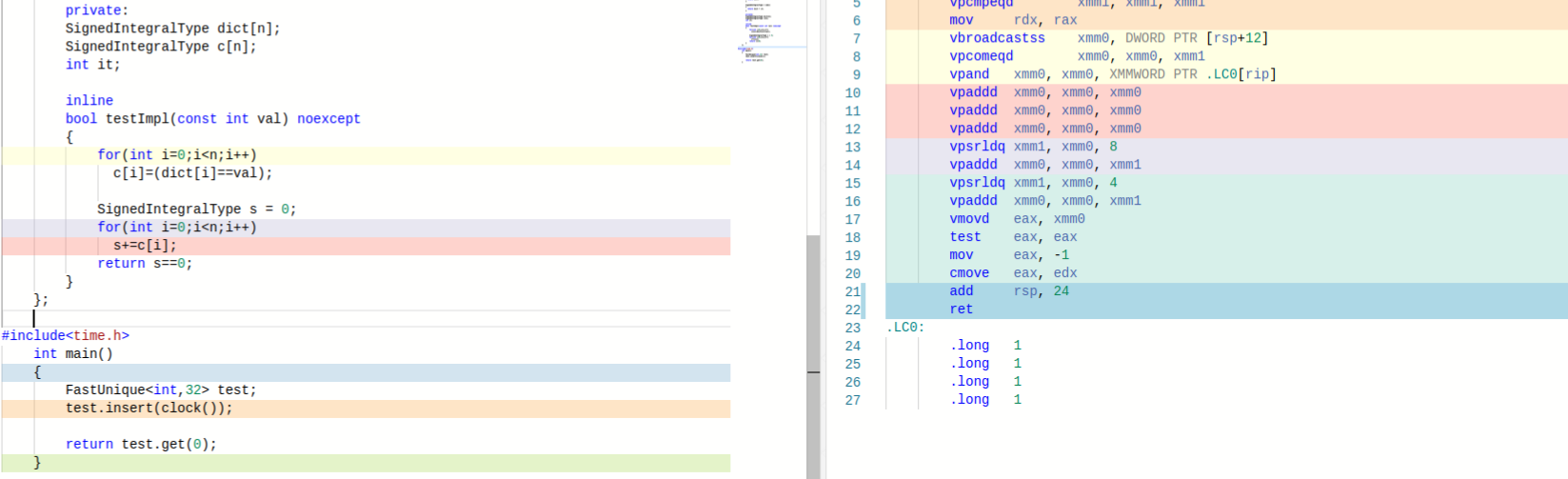
Since the number of particles per leaf node is limited to 32, the implementation works only for scenes with less than 33 overlappings on same cell of grid. With this limitation, duplication-removal after SIMD computations is reduced by a fast vectorized unique value accumulator (as fast as 10-20 cycles per insertion):
// keeps record of unique values inserted
// works for positive integers (-1 reserved for first comparisons)
template<typename SignedIntegralType, int n>
struct FastUnique
{
public:
FastUnique()
{
it=0;
for(int i=0;i<n;i++)
dict[i]=-1;
}
inline
void reset()
{
it=0;
for(int i=0;i<n;i++)
dict[i]=-1;
}
inline
void insert(const SignedIntegralType val)
{
const bool result = testImpl(val);
dict[it]=(result?val:dict[it]);
it+=(result?1:0);
}
inline
const SignedIntegralType get(const int index) const noexcept
{
return dict[index];
}
inline
const bool test(const SignedIntegralType val) noexcept
{
return testImpl(val);
}
inline
const void iterateSet(const SignedIntegralType val) noexcept
{
dict[it++]=val;
}
const int size()
{
return it;
}
SignedIntegralType * begin()
{
return dict;
}
SignedIntegralType * end()
{
return dict + it;
}
private:
SignedIntegralType dict[n];
SignedIntegralType c[n];
int it;
inline
bool testImpl(const int val) noexcept
{
for(int i=0;i<n;i++)
c[i]=(dict[i]==val);
SignedIntegralType s = 0;
for(int i=0;i<n;i++)
s+=c[i];
return s==0;
}
};
Despite the time complexity of O(N), this becomes much faster than std::unordered_set and std::unordered_map due to cache-aware and simd-aware code path which is successfully vectorized by the compiler to do 4/8/16 duplication checks per cycle:
With the vectorized 4x4 chunk collision test and the fast unique value container, the all-pairs adaptive grid collision detection algorithm is written:
Pseudo-code:
Iterate leaf-node array
gather all particle data into contiguous memory
divide the work into 4-sized chunks
for each 4-sized chunk
for each 4-sized chunk
compute collision for 16 different combinations at once
gather results into a deduplication container (multiple cells have same part)
write deduplicated id values into memory pool
copy memory pool content to result vector
Real-code:
// visits all leaf nodes (their offsets already found)and computes nxn collision pairs
std::vector<std::pair<int,int>> findCollisionsAll()
{
const int resetN = fields->mem.indexParticle.size();
fields->mem.allPairsCollmapping.allocate(resetN);
for(int i=0;i<resetN;i++)
{
fields->mem.allPairsCollmapping.getRef(i).reset();
}
fields->mem.allPairsCollmapping.reset();
fields->mem.allPairsColl.reset();
std::vector<std::pair<int,int>> result;
// using the leaf-list from tree-building phase
const int numLeaf = fields->mem.leafOffset.size();
for(int leaf=0;leaf<numLeaf;leaf++)
{
// prepare linear memory for all particles
{
const int leafOfs = fields->mem.leafOffset.get(leaf);
const int ptr = fields->mem.index.get(leafOfs);
const int n = fields->mem.index.get(leafOfs+1);
alignas(32)
int index[testParticleLimit];
alignas(32)
int orderId[testParticleLimit];
alignas(32)
int partId[testParticleLimit];
alignas(32)
float minx[testParticleLimit];
alignas(32)
float miny[testParticleLimit];
alignas(32)
float minz[testParticleLimit];
alignas(32)
float maxx[testParticleLimit];
alignas(32)
float maxy[testParticleLimit];
alignas(32)
float maxz[testParticleLimit];
constexpr int simd = 4;
constexpr int simd1 = simd-1;
const int n8 = n-(n&simd1);
for(int i=0;i<n8;i+=simd)
{
for(int j=0;j<simd;j++)
index[i+j] = ptr + i + j;
for(int j=0;j<simd;j++)
orderId[i+j] = fields->mem.orderParticle.get(index[i+j]);
for(int j=0;j<simd;j++)
partId[i+j] = fields->mem.indexParticle.get(orderId[i+j]);
for(int j=0;j<simd;j++)
minx[i+j] = fields->mem.minX.get(orderId[i+j]);
for(int j=0;j<simd;j++)
miny[i+j] = fields->mem.minY.get(orderId[i+j]);
for(int j=0;j<simd;j++)
minz[i+j] = fields->mem.minZ.get(orderId[i+j]);
for(int j=0;j<simd;j++)
maxx[i+j] = fields->mem.maxX.get(orderId[i+j]);
for(int j=0;j<simd;j++)
maxy[i+j] = fields->mem.maxY.get(orderId[i+j]);
for(int j=0;j<simd;j++)
maxz[i+j] = fields->mem.maxZ.get(orderId[i+j]);
}
for(int i=n8;i<n;i++)
{
index[i] = ptr + i;
orderId[i] = fields->mem.orderParticle.get(index[i]);
partId[i] = fields->mem.indexParticle.get(orderId[i]);
minx[i] = fields->mem.minX.get(orderId[i]);
miny[i] = fields->mem.minY.get(orderId[i]);
minz[i] = fields->mem.minZ.get(orderId[i]);
maxx[i] = fields->mem.maxX.get(orderId[i]);
maxy[i] = fields->mem.maxY.get(orderId[i]);
maxz[i] = fields->mem.maxZ.get(orderId[i]);
}
for(int i=n;i<testParticleLimit;i++)
{
index[i] = -1;
orderId[i] = -1;
partId[i] = -1;
minx[i] = 1000000000000000000.0f;
miny[i] = 1000000000000000000.0f;
minz[i] = 1000000000000000000.0f;
maxx[i] = 1000000000000000000.0f;
maxy[i] = 1000000000000000000.0f;
maxz[i] = 1000000000000000000.0f;
}
// SIMD computation (tiled computing)
{
alignas(32)
int out[16]={
0,0,0,0,
0,0,0,0,
0,0,0,0,
0,0,0,0
};
for(int i=0;i<testParticleLimit-simd;i+=simd)
{
if(i>=n)
break;
FastUnique<int32_t, testParticleLimit> * map[simd] = {
partId[i]>=0?fields->mem.allPairsCollmapping.getPtr(partId[i]):nullptr,
partId[i+1]>=0?fields->mem.allPairsCollmapping.getPtr(partId[i+1]):nullptr,
partId[i+2]>=0?fields->mem.allPairsCollmapping.getPtr(partId[i+2]):nullptr,
partId[i+3]>=0?fields->mem.allPairsCollmapping.getPtr(partId[i+3]):nullptr
};
for(int j=i;j<testParticleLimit;j+=simd)
{
if(j>=n)
break;
// 0v0, 0v1, 0v2, 0v3,
// 1v0, 1v1, 1v2, 1v3,
// 2v0, 2v1, 2v2, 2v3,
// 3v0, 3v1, 3v2, 3v3,
comp4vs4( partId+i, partId+j,
minx+i, minx+j,
miny+i, miny+j,
minz+i, minz+j,
maxx+i, maxx+j,
maxy+i, maxy+j,
maxz+i, maxz+j,
out
);
for(int k=0;k<16;k++)
{
const int k3 = k&3;
const int id2 = j+(k>>2);
if(out[k])
{
if(map[k3])
map[k3]->insert(partId[id2]);
}
}
}
}
}
}
}
// scan all unique values and insert into the memory pool
for(int i=0;i<resetN;i++)
{
FastUnique<int32_t, testParticleLimit>& map = fields->mem.allPairsCollmapping.getRef(i);
const int ms = map.size();
const int allocIdx = fields->mem.allPairsColl.allocate(ms);
for(int j=0;j<ms;j++)
{
fields->mem.allPairsColl.set(allocIdx+j,std::pair<int,int>(fields->mem.indexParticle.get(i),fields->mem.indexParticle.get(map.get(j))));
}
}
// copy content to result vector
result.resize(fields->mem.allPairsColl.size());
fields->mem.allPairsColl.writeTo(result);
return result;
}
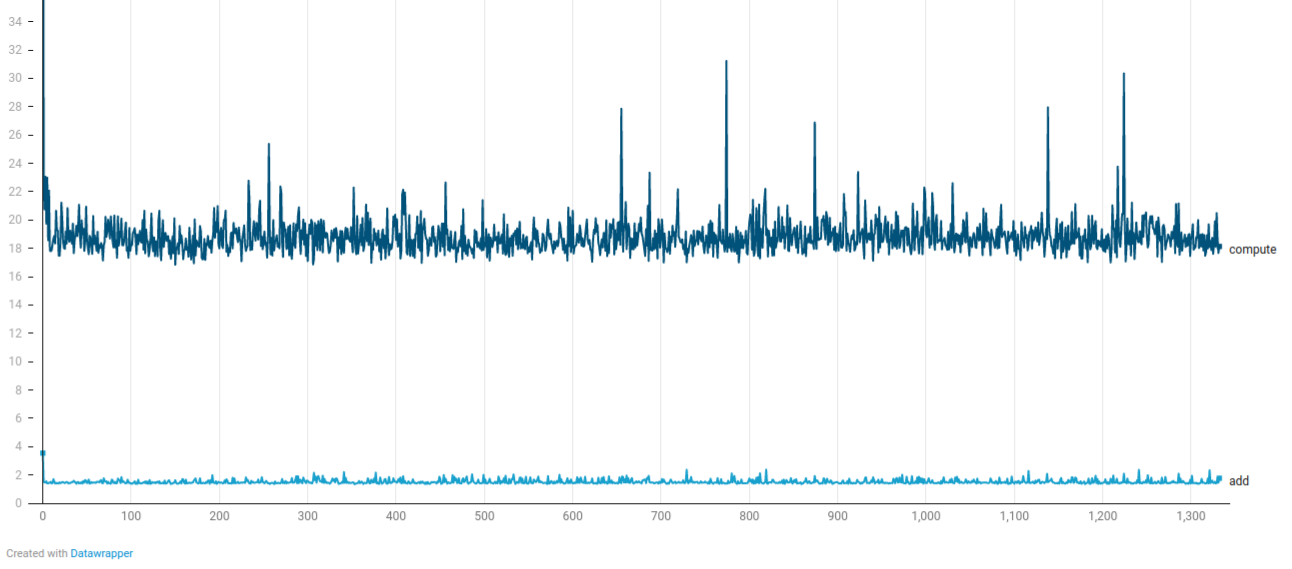
Random start, random movement, 20000 particles, 10000+ collisions each timestep
Y-axis: milliseconds
X-axis: timesteps
With only two time steps being slower than 60 FPS within 1500 timesteps, the single-threaded sparse-linear-adaptive-grid solution shows better performance scaling with increasing number of collisions (from 9000 to 14000) compared to the multi-threaded & simple approach. API interaction is similar:
// instantiate memory pool (not to be shared between multiple grids)
FastColDetLib::MemoryPool memPool;
// map cube volume of (-1, -1, -1) - (1, 1, 1) for collision computations
FastColDetLib::AdaptiveGridV2 grid(memPool,-1,-1,-1,1,1,1);
// physics simulation loop
while(true)
{
// O(1) complexity
grid.clear();
// par is vector of objects that implement IParticle<float> interface
grid.addParticles(n,par->data());
// O(num_particle * num_average_duplicates) complexity
grid.buildTree();
// O(num_particle * num_average_duplicates * 32 * 32) complexity
std::vector<std::pair<int,int>> collisions = grid.findCollisionsAll();
// make collided particles bounce back
physics_calc(collisions);
}
Even with much better per-thread performance compared to the first solution, it is still harder to add multithreading to the tree-building phase which makes it a limiting factor for scaling. As another way, each thread can have its own adaptive grid mapped to a different section of the targeted volume. This can make unbalanced workload between cores if particles are not distributed evenly to all quadrants.
The SOA node representation (each field having its own array) can be modified to use SIMD during tree traversal for computing collisions of a particle with all child-nodes of current node. This may or may not add performance to the non-all-pair collision detection method:
std::vector<int> findCollisions(
const float minx, const float miny, const float minz,
const float maxx, const float maxy, const float maxz
);
Currently, it is not optimized to use any SIMD nor multithreading and is slower than all-pair computations for 20000 particles (more than 2 microseconds per particle).
The all-pair computation method does not traverse the tree but does a simple iteration over a leaf-array, this way it does not require tree-traversal optimization currently.
Online Tests For Newer CPUs
The development computer's processor (FX8150 at 2.1GHz) is used to simulate very old CPUs with SSE native-width of SIMD units. To get a better view of newer CPU generations, online C++ compiler services are used for the following code:
#include"FastCollisionDetectionLib.h"
#include<atomic>
#include<iostream>
template<typename CoordType>
struct Vector3D
{
CoordType x,y,z;
Vector3D<CoordType> crossProduct(Vector3D<CoordType> vec)
{
Vector3D<CoordType> res;
res.x = y*vec.z - z*vec.y;
res.y = z*vec.x - x*vec.z;
res.z = x*vec.y - y*vec.x;
return res;
}
Vector3D<CoordType> operator - (Vector3D<CoordType> vec)
{
Vector3D<CoordType> result;
result.x = x-vec.x;
result.y = y-vec.y;
result.z = z-vec.z;
return result;
}
Vector3D<CoordType> operator + (Vector3D<CoordType> vec)
{
Vector3D<CoordType> result;
result.x = x+vec.x;
result.y = y+vec.y;
result.z = z+vec.z;
return result;
}
Vector3D<CoordType> operator * (CoordType v)
{
Vector3D<CoordType> result;
result.x = x*v;
result.y = y*v;
result.z = z*v;
return result;
}
// warning: sqrt is not necessary in production code like:
// if ( v1.abs()<v2.abs() ) { .. }
// the sqrt below is intentionally left to simulate "heavy" task in "challenge 1"
CoordType abs()
{
return std::sqrt(x*x+y*y+z*z);
}
};
template<typename CoordType>
struct PointCloud
{
Vector3D<CoordType> point[125];
PointCloud(CoordType x, CoordType y, CoordType z)
{
for(int i=0;i<125;i++)
{
point[i].x=x+i%5-2.5f;
point[i].y=y+(i/5)%5-2.5f;
point[i].z=z+i/25-2.5f;
}
}
};
template<typename CoordType>
bool pointCloudIntersection(PointCloud<CoordType>& cl1, PointCloud<CoordType>& cl2)
{
for(Vector3D<CoordType>& p:cl1.point)
{
for(Vector3D<CoordType>& p2:cl2.point)
{
if((p-p2).abs()<1.0f)
{
return true;
}
}
}
return false;
}
template<typename CoordType>
bool intersectDim(const CoordType minx, const CoordType maxx, const CoordType minx2, const CoordType maxx2)
{
return !((maxx < minx2) || (maxx2 < minx));
}
#include"Generator.h"
template<typename CoordType>
struct AABBofPointCloud: public FastColDetLib::IParticle<CoordType>
{
AABBofPointCloud(int idPrm, PointCloud<CoordType> * pCloudPrm)
{
id=idPrm;
pCloud = pCloudPrm;
xmin=pCloud->point[0].x;
ymin=pCloud->point[0].y;
zmin=pCloud->point[0].z;
xmax=pCloud->point[0].x;
ymax=pCloud->point[0].y;
zmax=pCloud->point[0].z;
for(int i=0;i<125;i++)
{
if(xmin>pCloud->point[i].x)
xmin=pCloud->point[i].x;
if(ymin>pCloud->point[i].y)
ymin=pCloud->point[i].y;
if(zmin>pCloud->point[i].z)
zmin=pCloud->point[i].z;
if(xmax<pCloud->point[i].x)
xmax=pCloud->point[i].x;
if(ymax<pCloud->point[i].y)
ymax=pCloud->point[i].y;
if(zmax<pCloud->point[i].z)
zmax=pCloud->point[i].z;
}
}
int id;
PointCloud<CoordType>* pCloud;
CoordType xmin;
CoordType ymin;
CoordType zmin;
CoordType xmax;
CoordType ymax;
CoordType zmax;
const CoordType getMaxX()const {return xmax;}
const CoordType getMaxY()const {return ymax;}
const CoordType getMaxZ()const {return zmax;}
const CoordType getMinX()const {return xmin;}
const CoordType getMinY()const {return ymin;}
const CoordType getMinZ()const {return zmin;}
const int getId()const {return id;}
};
int main()
{
using cotype = float;
PointCloud<cotype> ico1(0,0,0);
// heating the CPU for benchmarking
for(int i=0;i<10000;i++)
{
PointCloud<cotype> ico2(0,0.1f,i*0.1f);
pointCloudIntersection(ico1,ico2);
}
const int N = 20004;
std::vector<PointCloud<cotype>> objects;
oofrng::Generator<64> gen;
for(int i=0;i<N-3;i++)
{
objects.push_back(PointCloud<cotype>(gen.generate1Float()*900,gen.generate1Float()*900,gen.generate1Float()*900));
}
// the teapot in stadium problem
objects.push_back(PointCloud<cotype>(9000,9000,9000));
objects.push_back(PointCloud<cotype>(9001,9001,9001));
objects.push_back(PointCloud<cotype>(9002,9002,9002));
std::vector<AABBofPointCloud<cotype>> AABBs;
for(int i=0;i<N;i++)
{
AABBs.push_back(AABBofPointCloud<cotype>(i,&objects[i]));
}
FastColDetLib::MemoryPool memPool;
FastColDetLib::AdaptiveGridV2 grid2_0(memPool,0,0,0,10005,10005,10005);
// benchmark begin
for(int j=0;j<15;j++)
{
size_t nano;
std::map<int,std::map<int,bool>> collisionMatrix;
{
std::atomic<int> ctr;
ctr.store(0);
{
{
FastColDetLib::Bench bench(&nano);
{
size_t t1,t2,t3;
{
FastColDetLib::Bench b(&t1);
grid2_0.clear();
}
{
FastColDetLib::Bench b(&t2);
grid2_0.addParticles(N,AABBs.data());
}
{
FastColDetLib::Bench b(&t3);
grid2_0.buildTree();
}
std::cout<<t1<<" "<<t2<<" "<<t3<<std::endl;
auto vec = grid2_0.findCollisionsAll();
ctr += vec.size();
}
}
std::cout<<N<<" vs "<<N<<" AABB collision checking by adaptive grid= "<<nano<<" nanoseconds "<<std::endl;
std::cout<<"total = "<<ctr.load()<<std::endl;
}
}
}
return 0;
}
FX8150 at 2.1GHz, single thread
1287 1715939 17096316 20004 vs 20004 AABB collision checking by adaptive grid= 42595898 nanoseconds total = 137 1808 494565 6036179 20004 vs 20004 AABB collision checking by adaptive grid= 11770599 nanoseconds total = 137 1388 519662 5873310 20004 vs 20004 AABB collision checking by adaptive grid= 11552612 nanoseconds total = 137 1423 552296 5892499 20004 vs 20004 AABB collision checking by adaptive grid= 11380779 nanoseconds total = 137 1163 450733 6186093 20004 vs 20004 AABB collision checking by adaptive grid= 11733104 nanoseconds total = 137 1251 491513 5952507 20004 vs 20004 AABB collision checking by adaptive grid= 11333729 nanoseconds total = 137 1121 448833 5891781 20004 vs 20004 AABB collision checking by adaptive grid= 11225727 nanoseconds total = 137 1291 476826 6144553 20004 vs 20004 AABB collision checking by adaptive grid= 11609930 nanoseconds total = 137 1236 480449 5921570 20004 vs 20004 AABB collision checking by adaptive grid= 11278574 nanoseconds total = 137 1167 450557 5862713 20004 vs 20004 AABB collision checking by adaptive grid= 11278160 nanoseconds total = 137 1234 472445 6146572 20004 vs 20004 AABB collision checking by adaptive grid= 11617215 nanoseconds total = 137 1304 479957 5932065 20004 vs 20004 AABB collision checking by adaptive grid= 11248743 nanoseconds total = 137 1271 463188 5910676 20004 vs 20004 AABB collision checking by adaptive grid= 11265749 nanoseconds total = 137 5271 508218 6104409 20004 vs 20004 AABB collision checking by adaptive grid= 11581773 nanoseconds total = 137 1243 478395 5910560 20004 vs 20004 AABB collision checking by adaptive grid= 11396155 nanoseconds total = 137
With only 137 collisions, sum of run-time of clearing, particle-insertion, tree building and all-pair computation takes less than 11.5 milliseconds on average while half of the time is spent on building the tree.
AVX2 (Xeon E-2286G 4GHz), single thread
331 269690 4106238 20004 vs 20004 AABB collision checking by adaptive grid= 11095752 nanoseconds total = 137 610 133017 1431199 20004 vs 20004 AABB collision checking by adaptive grid= 3702480 nanoseconds total = 137 203 137703 1327516 20004 vs 20004 AABB collision checking by adaptive grid= 3615986 nanoseconds total = 137 231 126511 1332285 20004 vs 20004 AABB collision checking by adaptive grid= 3599439 nanoseconds total = 137 231 122653 1334227 20004 vs 20004 AABB collision checking by adaptive grid= 3601913 nanoseconds total = 137 316 112752 1300873 20004 vs 20004 AABB collision checking by adaptive grid= 3559040 nanoseconds total = 137 256 125327 1298195 20004 vs 20004 AABB collision checking by adaptive grid= 3544539 nanoseconds total = 137 265 121138 1241168 20004 vs 20004 AABB collision checking by adaptive grid= 3505718 nanoseconds total = 137 205 125888 1292359 20004 vs 20004 AABB collision checking by adaptive grid= 3505236 nanoseconds total = 137 277 129064 1310662 20004 vs 20004 AABB collision checking by adaptive grid= 3548348 nanoseconds total = 137 333 124409 1309687 20004 vs 20004 AABB collision checking by adaptive grid= 3546196 nanoseconds total = 137 249 125756 1313174 20004 vs 20004 AABB collision checking by adaptive grid= 3544577 nanoseconds total = 137 227 123104 1335686 20004 vs 20004 AABB collision checking by adaptive grid= 3565008 nanoseconds total = 137 330 97679 1296398 20004 vs 20004 AABB collision checking by adaptive grid= 3490028 nanoseconds total = 137 282 97633 1294944 20004 vs 20004 AABB collision checking by adaptive grid= 3518168 nanoseconds total = 137
Completing all of tasks in 3.5 milliseconds is 3.3x performance, nearly all of the speedup gained from higher instructions per second performance of new processor and its higher working frequency. Having only 137 collisions does not benefit enough from SIMD capability.
AVX512 (Xeon Gold 5115 and Xeon Gold 5215), single thread
(-Wall -std=c++14 -O3 -march=native -mavx512f -ftree-vectorize -ffast-math -o a.out source_file.cpp)
712 923026 13887800 20004 vs 20004 AABB collision checking by adaptive grid= 39407342 nanoseconds total = 137 1818 404930 5271792 20004 vs 20004 AABB collision checking by adaptive grid= 20791697 nanoseconds total = 137 1976 374333 6295718 20004 vs 20004 AABB collision checking by adaptive grid= 12459388 nanoseconds total = 137 1820 433518 5018476 20004 vs 20004 AABB collision checking by adaptive grid= 13907910 nanoseconds total = 137 1836 394659 5168525 20004 vs 20004 AABB collision checking by adaptive grid= 11257770 nanoseconds total = 137 1360 721575 5573255 20004 vs 20004 AABB collision checking by adaptive grid= 12274256 nanoseconds total = 137 1283 872188 5019439 20004 vs 20004 AABB collision checking by adaptive grid= 11718171 nanoseconds total = 137 1065 370593 3192312 20004 vs 20004 AABB collision checking by adaptive grid= 7165426 nanoseconds total = 137 2243 222700 3017543 20004 vs 20004 AABB collision checking by adaptive grid= 7580070 nanoseconds total = 137 12110 252045 3169418 20004 vs 20004 AABB collision checking by adaptive grid= 7609170 nanoseconds total = 137 1902 483356 3613861 20004 vs 20004 AABB collision checking by adaptive grid= 8001453 nanoseconds total = 137 1161 270468 2927408 20004 vs 20004 AABB collision checking by adaptive grid= 6765911 nanoseconds total = 137 1534 721745 3550246 20004 vs 20004 AABB collision checking by adaptive grid= 9669111 nanoseconds total = 137 1465 374488 4659102 20004 vs 20004 AABB collision checking by adaptive grid= 10340249 nanoseconds total = 137 1061 226212 3145650 20004 vs 20004 AABB collision checking by adaptive grid= 7007133 nanoseconds total = 137
The last two tests indicate that CPU frequency and IPC are more important when there are not many collisions.
Same tests with dense collisions by changing few lines of code:
objects.push_back(
PointCloud<cotype>(
gen.generate1Float()*900,gen.generate1Float()*900,gen.generate1Float()*900)
);
to:
objects.push_back(
PointCloud<cotype>(
gen.generate1Float()*150,gen.generate1Float()*150,gen.generate1Float()*150)
);
FX8150 at 2.1GHz, single thread
809 1137072 16250322 20004 vs 20004 AABB collision checking by adaptive grid= 45634949 nanoseconds total = 29326 11628 774879 6375167 20004 vs 20004 AABB collision checking by adaptive grid= 17535811 nanoseconds total = 29326 1323 489172 6242101 20004 vs 20004 AABB collision checking by adaptive grid= 16964760 nanoseconds total = 29326 1439 503646 6378985 20004 vs 20004 AABB collision checking by adaptive grid= 17205537 nanoseconds total = 29326 1430 507256 6200894 20004 vs 20004 AABB collision checking by adaptive grid= 16871454 nanoseconds total = 29326 1292 480034 6326381 20004 vs 20004 AABB collision checking by adaptive grid= 17126909 nanoseconds total = 29326 1471 494320 6234695 20004 vs 20004 AABB collision checking by adaptive grid= 16951342 nanoseconds total = 29326 1438 507194 6376321 20004 vs 20004 AABB collision checking by adaptive grid= 17215743 nanoseconds total = 29326 1439 510082 6213300 20004 vs 20004 AABB collision checking by adaptive grid= 16906657 nanoseconds total = 29326 1294 588172 6218907 20004 vs 20004 AABB collision checking by adaptive grid= 17530016 nanoseconds total = 29326 1512 479942 6271097 20004 vs 20004 AABB collision checking by adaptive grid= 17305008 nanoseconds total = 29326 1364 491258 6211765 20004 vs 20004 AABB collision checking by adaptive grid= 17117965 nanoseconds total = 29326 1400 484784 6234349 20004 vs 20004 AABB collision checking by adaptive grid= 18445534 nanoseconds total = 29326 2177 915668 7516056 20004 vs 20004 AABB collision checking by adaptive grid= 18903198 nanoseconds total = 29326 1610 658380 6986867 20004 vs 20004 AABB collision checking by adaptive grid= 20395348 nanoseconds total = 29326
Gets 10% slower than 60FPS with 29326 collisions (on average 1.5 particles touching each particle), with tree-building taking only ~1/3 of run-time.
AVX2 (Xeon E-2286G 4GHz), single thread (https://wandbox.org/permlink/tdGggzzAkHN3VkUz)
702 270682 4482552 20004 vs 20004 AABB collision checking by adaptive grid= 18340629 nanoseconds total = 29326 15704 134363 1598335 20004 vs 20004 AABB collision checking by adaptive grid= 10920371 nanoseconds total = 29326 377 140370 1546184 20004 vs 20004 AABB collision checking by adaptive grid= 10877674 nanoseconds total = 29326 271 118858 1518309 20004 vs 20004 AABB collision checking by adaptive grid= 10822341 nanoseconds total = 29326 582 128086 1539374 20004 vs 20004 AABB collision checking by adaptive grid= 10880007 nanoseconds total = 29326 293 128848 1534561 20004 vs 20004 AABB collision checking by adaptive grid= 10841986 nanoseconds total = 29326 606 129491 1546189 20004 vs 20004 AABB collision checking by adaptive grid= 10877790 nanoseconds total = 29326 215 127919 1545995 20004 vs 20004 AABB collision checking by adaptive grid= 10781822 nanoseconds total = 29326 214 126475 1528446 20004 vs 20004 AABB collision checking by adaptive grid= 10830309 nanoseconds total = 29326 296 115932 1547976 20004 vs 20004 AABB collision checking by adaptive grid= 10863433 nanoseconds total = 29326 273 127565 1529545 20004 vs 20004 AABB collision checking by adaptive grid= 10829295 nanoseconds total = 29326 247 127836 1554261 20004 vs 20004 AABB collision checking by adaptive grid= 10938447 nanoseconds total = 29326 241 100625 1541077 20004 vs 20004 AABB collision checking by adaptive grid= 10936425 nanoseconds total = 29326 251 100587 1545350 20004 vs 20004 AABB collision checking by adaptive grid= 10903145 nanoseconds total = 29326 526 101546 1542023 20004 vs 20004 AABB collision checking by adaptive grid= 10916791 nanoseconds total = 29326
AVX2 CPU with 2x frequency achieves 91 FPS. 1.5milliseconds tree-building and 9.3 milliseconds all-pair computation.
AVX512 (Xeon Gold 5115 and Xeon Gold 5215), single thread (https://rextester.com/YKDN52107)
463 638674 8377763 20004 vs 20004 AABB collision checking by adaptive grid= 28530573 nanoseconds total = 29326 1995 222204 2649192 20004 vs 20004 AABB collision checking by adaptive grid= 12960779 nanoseconds total = 29326 1538 222590 2658591 20004 vs 20004 AABB collision checking by adaptive grid= 12791377 nanoseconds total = 29326 1378 218950 2662630 20004 vs 20004 AABB collision checking by adaptive grid= 13005473 nanoseconds total = 29326 1256 217816 2639028 20004 vs 20004 AABB collision checking by adaptive grid= 12879503 nanoseconds total = 29326 1272 232140 2625833 20004 vs 20004 AABB collision checking by adaptive grid= 12799225 nanoseconds total = 29326 956 225068 2634176 20004 vs 20004 AABB collision checking by adaptive grid= 12939098 nanoseconds total = 29326 1292 217455 2665934 20004 vs 20004 AABB collision checking by adaptive grid= 12769266 nanoseconds total = 29326 1386 220565 2686391 20004 vs 20004 AABB collision checking by adaptive grid= 12779806 nanoseconds total = 29326 1735 219911 2656253 20004 vs 20004 AABB collision checking by adaptive grid= 12820786 nanoseconds total = 29326 1153 216455 2638674 20004 vs 20004 AABB collision checking by adaptive grid= 12742196 nanoseconds total = 29326 1123 236914 2633897 20004 vs 20004 AABB collision checking by adaptive grid= 12872167 nanoseconds total = 29326 1971 219628 2642318 20004 vs 20004 AABB collision checking by adaptive grid= 12864358 nanoseconds total = 29326 1181 215090 2676025 20004 vs 20004 AABB collision checking by adaptive grid= 12990054 nanoseconds total = 29326 1291 215507 2653345 20004 vs 20004 AABB collision checking by adaptive grid= 12841870 nanoseconds total = 29326
Xeon Gold 5215 reaches 78 FPS with 2.9GHz turbo (27.5% less CPU frequency than AVX2 test) that is 15% slower than the 4GHz AVX2 test. 2.6 milliseconds tree-building and 10.2 milliseconds all-pair computation.
The tests indicate that there are still heavy bottlenecks on parts other than the vectorized all-pair computations. One of the most speed-dropping effects is RAM latency when cache misses are still high when there are too many duplicates in the computed region. Despite removing duplicates, accessing the duplicated data still evicts too many useful data from cache to RAM and causes less scaling between different CPUs.
The implementation doesn't benefit from SIMD in tree-building (yet). This makes 1 extra millisecond of tree-building in AVX512 test compared to 4GHz AVX2 test. This makes nearly 25% per-cycle performance gain in the all-pair collision computation method for the AVX512 test.
With 12000 and 6400 collisions, Xeon Gold(AVX512) reaches 97 FPS and 100 FPS and this shows higher-bound of performance (100 FPS) due to the bottlenecks found in tree-building, particle insertion (and possibly in all-pair computation).
All AVX2 and AVX512 tests were run through online C++ compiler servers that are shared by multiple clients and real performance can be higher or lower depending on server load.
All-Pairs Collision Test For 40k AABBs at 60 FPS
To add more performance without significantly changing the original adaptive grid implementation, an external header file is written with simple octree-like structure to find multiple clusters of particles and bind them to different dedicated compute-threads.
Psudo-code for new algorithm:
put particles into root node
recursive_compute(this):
if number of particles in this node > 10000
create 64 children nodes (4x4x4 grid)
put particles into all possibly-overlapping child nodes
for all child nodes
recursive_compute(node)
else
create new task for a dedicated thread
create adaptive grid for particles of this node
compute all-pairs collision
if this node is root
wait for all dedicated threads to finish tasks
blend all results from all adaptive grids (deduplication/insertion)
return unified results
collisions = recursive_compute(root)
The tree structure in the source code is half-linearized & half-conventional to keep complexity lower than adaptive-grid implementation and performance higher than conventional tree.
Due to the single-threaded construction of load-balancer tree (AdaptiveGridTree<numThreads>), the load balancing is only efficient when tree-depth of particles are not too high. When too many particles represent "teapot in stadium" problem, this causes too much tree traversal & construction on single thread and makes multithreaded performance-scaling inefficient.
Currently, the implementation uses 10000 as a critical point of number of particles per node for branching for not losing too much performance due to limited cache size of CPU cores:
#ifndef ADAPTIVEGRIDTREE_H_
#define ADAPTIVEGRIDTREE_H_
#include<atomic>
#include<thread>
#include<mutex>
#include<functional>
#include"FastCollisionDetectionLib.h"
// simple dense octree
constexpr int numNodesPerNode = 64;
struct GridTreeNode
{
GridTreeNode()
{
for(int i=0;i<numNodesPerNode;i++)
childNodes[i]=nullptr;
}
std::shared_ptr<GridTreeNode> childNodes[numNodesPerNode];
std::vector<int> parOrder;
};
template<int concurrency>
class AdaptiveGridTree
{
public:
AdaptiveGridTree(const float minx, const float miny, const float minz, const float maxx, const float maxy, const float maxz):
minX(minx),minY(miny),minZ(minz),maxX(maxx),maxY(maxy),maxZ(maxz), workCtr(0)
{
for(int i=0;i<concurrency;i++)
{
thr.emplace_back([&](){
FastColDetLib::MemoryPool mem;
bool work=true;
while(work)
{
auto f = taskQueue.pop();
if(f)
{
f(mem);
taskCompleteQueue.push2(true);
}
else
break;
}
taskCompleteQueue.push(true);
});
}
}
~AdaptiveGridTree()
{
for(int i=0;i<concurrency*2;i++)
taskQueue.push(nullptr);
for(int i=0;i<concurrency;i++)
{
thr[i].join();
}
}
void clear()
{
std::lock_guard<std::mutex> lg(mut);
parId.reset();
parMinX.reset();
parMinY.reset();
parMinZ.reset();
parMaxX.reset();
parMaxY.reset();
parMaxZ.reset();
}
template<typename Derived>
void addParticles(const int N, Derived * ptr)
{
std::lock_guard<std::mutex> lg(mut);
const int ofsId = parId.allocate(N);
const int ofsMinx = parMinX.allocate(N);
const int ofsMiny = parMinY.allocate(N);
const int ofsMinz = parMinZ.allocate(N);
const int ofsMaxx = parMaxX.allocate(N);
const int ofsMaxy = parMaxY.allocate(N);
const int ofsMaxz = parMaxZ.allocate(N);
for(int i=0;i<N;i++)
{
parId.set(ofsId+i,static_cast<FastColDetLib::IParticle<float>*>(ptr+i)->getId());
parMinX.set(ofsMinx+i,static_cast<FastColDetLib::IParticle<float>*>(ptr+i)->getMinX());
parMinY.set(ofsMiny+i,static_cast<FastColDetLib::IParticle<float>*>(ptr+i)->getMinY());
parMinZ.set(ofsMinz+i,static_cast<FastColDetLib::IParticle<float>*>(ptr+i)->getMinZ());
parMaxX.set(ofsMaxx+i,static_cast<FastColDetLib::IParticle<float>*>(ptr+i)->getMaxX());
parMaxY.set(ofsMaxy+i,static_cast<FastColDetLib::IParticle<float>*>(ptr+i)->getMaxY());
parMaxZ.set(ofsMaxz+i,static_cast<FastColDetLib::IParticle<float>*>(ptr+i)->getMaxZ());
}
}
std::vector<std::pair<int,int>> computeAllPairs(GridTreeNode * parent = nullptr, float minx=0.0f, float miny=0.0f, float minz=0.0f, float maxx=0.0f, float maxy=0.0f, float maxz=0.0f,
std::vector<std::pair<int,int>> * result=nullptr, FastColDetLib::Memory<FastColDetLib::FastUnique<int32_t,FastColDetLib::testUniqueLimit>> * mapping = nullptr)
{
GridTreeNode root;
std::vector<std::pair<int,int>> resultRoot;
if(!parent)
{
workCtr=0;
const int N = parId.size();
mappingRoot.reset();
mappingRoot.allocate(N);
minx = minX;
miny = minY;
minz = minZ;
maxx = maxX;
maxy = maxY;
maxz = maxZ;
parent = &root;
for(int i=0;i<N;i++)
{
parent->parOrder.push_back(i);
mappingRoot.getRef(i).reset();
}
result = &resultRoot;
mapping = &mappingRoot;
}
// build tree until 10k or less particles left for each leaf
if(parent->parOrder.size()>10000)
{
const int N = parent->parOrder.size();
for(int i=0;i<numNodesPerNode;i++)
{
parent->childNodes[i]=std::make_shared<GridTreeNode>();
}
const float stepx = 4.0f/(maxx - minx);
const float stepy = 4.0f/(maxy - miny);
const float stepz = 4.0f/(maxz - minz);
for(int i=0;i<numNodesPerNode;i++)
{
accumulator[i].reset();
}
for(int i=0;i<N;i++)
{
// calculate overlapping region's cell indices
const int parOrdI = parent->parOrder[i];
const int mincornerstartx = std::floor((parMinX.get(parOrdI) - minx) * stepx);
const int maxcornerendx = std::floor((parMaxX.get(parOrdI) - minx) * stepx);
const int mincornerstarty = std::floor((parMinY.get(parOrdI) - miny) * stepy);
const int maxcornerendy = std::floor((parMaxY.get(parOrdI) - miny) * stepy);
const int mincornerstartz = std::floor((parMinZ.get(parOrdI) - minz) * stepz);
const int maxcornerendz = std::floor((parMaxZ.get(parOrdI) - minz) * stepz);
for(int ii=mincornerstartz;ii<=maxcornerendz;ii++)
for(int j=mincornerstarty;j<=maxcornerendy;j++)
for(int k=mincornerstartx;k<=maxcornerendx;k++)
{
if(ii<0 || ii>=4 || j<0 || j>=4 || k<0 || k>=4)
continue;
auto & acc = accumulator[k+j*4+ii*16];
acc.set(acc.allocate(1), parOrdI);
}
}
{
for(int i=0;i<numNodesPerNode;i++)
{
const int n = accumulator[i].size();
for(int j=0;j<n;j++)
{
parent->childNodes[i]->parOrder.push_back(accumulator[i].get(j));
}
}
}
for(int i=0;i<numNodesPerNode;i++)
{
if(parent->childNodes[i]->parOrder.size()>1)
{
computeAllPairs(parent->childNodes[i].get(),
minx+(i&3)/stepx, miny+((i/4)&3)/stepy, minz+(i/16)/stepz,
minx+(i&3)/stepx + 1.0f/stepx, miny+((i/4)&3)/stepy + 1.0f/stepy, minz+(i/16)/stepz + 1.0f/stepz, result,mapping);
}
}
}
else
{
if(parent->parOrder.size()>1)
{
// offload to another thread as a sparse-linear-adaptive-grid
workCtr++;
taskQueue.push2([&,parent,minx,miny,minz,maxx,maxy,maxz,result](FastColDetLib::MemoryPool mem)
{
FastColDetLib::AdaptiveGridV2 subGrid(mem,minx,miny,minz,maxx,maxy,maxz);
subGrid.clear();
{
subGrid.addParticlesWithoutInterface(parent->parOrder.size(), 0, parent->parOrder,
parId,
parMinX, parMinY, parMinZ,
parMaxX, parMaxY, parMaxZ
);
subGrid.buildTree();
}
const std::vector<std::pair<int,int>> coll = subGrid.findCollisionsAll();
if(coll.size()>0)
{
std::lock_guard<std::mutex> lg(mut);
result->insert(result->end(),coll.begin(),coll.end());
}
});
}
}
if(parent == &root)
{
constexpr int mutN = 1024;
constexpr int mutN1 = mutN-1;
FastColDetLib::MutexWithoutFalseSharing mutArr[mutN];
int endQueue = 0;
while(endQueue<workCtr)
{
if(taskCompleteQueue.pop())
{
endQueue++;
}
}
workCtr = 0;
std::lock_guard<std::mutex> lg(mut);
resultRootMem.reset();
{
{
const int nr = resultRoot.size();
for(int i=0;i<nr;i+=1000)
{
workCtr++;
taskQueue.push2([&,i](FastColDetLib::MemoryPool & mem)
{
unsigned int lastId = 2000000000; // so you don't have 2 billion particles in a game right?
mutArr[lastId&mutN1].mut.lock();
for(int j=0;j<1000;j++)
{
if(i+j>=nr)
break;
const unsigned int rfirst = resultRoot[i+j].first;
const int rsecond = resultRoot[i+j].second;
if(lastId != rfirst)
{
//std::lock_guard<std::mutex> lg(mutArr[rfirst&255].mut);
mutArr[lastId&mutN1].mut.unlock();
mutArr[rfirst&mutN1].mut.lock();
mapping->getRef(rfirst).insert(rsecond);
lastId = rfirst;
}
else
{
//std::lock_guard<std::mutex> lg(mutArr[rfirst&255].mut);
mapping->getRef(rfirst).insert(rsecond);
}
}
mutArr[lastId&mutN1].mut.unlock();
});
}
endQueue = 0;
while(endQueue<workCtr)
{
if(taskCompleteQueue.pop())
{
endQueue++;
}
}
workCtr = 0;
}
resultRoot.clear();
const int N = mapping->size();
int allocSize = 0;
std::vector<std::pair<int,int>> allocOfs;
for(int i=0;i<N;i++)
{
//std::lock_guard<std::mutex> lg(mutArr[i&255].mut);
const int isz = mapping->getRef(i).size();
if(isz > 0)
{
allocOfs.push_back(std::pair<int,int>(i,allocSize));
allocSize += isz;
}
}
resultRootMem.allocate(allocSize);
const int N2 = allocOfs.size();
for(int i0=0;i0<N2;i0+=10000)
{
workCtr++;
taskQueue.push2([&,i0](FastColDetLib::MemoryPool & mem)
{
for(int j=0;j<10000;j++)
{
const int i = i0+j;
if(i>=N2)
break;
auto & ref = mapping->getRef(allocOfs[i].first);
const int n = ref.size();
const int ofs0 = allocOfs[i].second;
for(int j=0;j<n;j++)
{
resultRootMem.set(ofs0+j,std::pair<int,int>(allocOfs[i].first,ref.get(j)));
}
}
});
}
endQueue = 0;
while(endQueue<workCtr)
{
if(taskCompleteQueue.pop())
{
endQueue++;
}
}
workCtr = 0;
resultRoot.resize(resultRootMem.size());
resultRootMem.writeTo(resultRoot);
}
}
return resultRoot;
}
private:
std::mutex mut;
std::vector<std::thread> thr;
FastColDetLib::SyncQueue<std::function<void(FastColDetLib::MemoryPool &)>> taskQueue;
FastColDetLib::SyncQueue<bool> taskCompleteQueue;
FastColDetLib::Memory<std::pair<int,int>> resultRootMem;
FastColDetLib::Memory<FastColDetLib::FastUnique<int32_t,FastColDetLib::testUniqueLimit>> mappingRoot;
const float minX,minY,minZ,maxX,maxY,maxZ;
int workCtr;
FastColDetLib::Memory<int> parId;
FastColDetLib::Memory<float> parMinX;
FastColDetLib::Memory<float> parMinY;
FastColDetLib::Memory<float> parMinZ;
FastColDetLib::Memory<float> parMaxX;
FastColDetLib::Memory<float> parMaxY;
FastColDetLib::Memory<float> parMaxZ;
FastColDetLib::Memory<int> accumulator[numNodesPerNode];
};
#endif /* ADAPTIVEGRIDTREE_H_ */
Benchmark timings for particle-insertion + tree building and all-pairs computation on FX8150 2.1GHz + 4GB DDR3 1333MHz RAM with 40000 randomly moving & randomly placed particles doing 1100 collisions total:
Randomly distributed particles do not cause any more depth than 1 for the load-balancer tree. The root node has 64 child nodes each with less than 10000 particles (40000/64 on average) and their tasks pushed into a common task queue that is consumed by 7 threads (while 1 thread is left for the control logic for benchmarking) concurrently.
Shallow tree is built under 2 milliseconds and computations are completed under 18 milliseconds with 14.5 milliseconds as average. On average, this is 60 FPS but contains performance spikes due to chaotic work allocations caused by chaotic movements of particles.
When number of collisions are increased from 1100 to 29000, performance drops below 50 FPS:
This is mainly caused by deduplication part of the load balancer tree where different results from all adaptive grids are merged with no duplicated collision pair. 29000 collisions for 40000 particles is equivalent to 3/4 of all particles having single collision pair and has below image for rendering:
(Red dots are colliding particles, white dots are non-colliding particles.)
Same performance is retained until 49000 collisions. With 118000 collisions, FPS drops to 35.
In teapot-in-stadium problem with shallower tree-depth:
( particles are fit inside a wider region of one of dimensions, compared to latest single-thread benchmark)
#include"FastCollisionDetectionLib.h"
#include<atomic>
#include<iostream>
template<typename CoordType>
struct Vector3D
{
CoordType x,y,z;
Vector3D<CoordType> crossProduct(Vector3D<CoordType> vec)
{
Vector3D<CoordType> res;
res.x = y*vec.z - z*vec.y;
res.y = z*vec.x - x*vec.z;
res.z = x*vec.y - y*vec.x;
return res;
}
Vector3D<CoordType> operator - (Vector3D<CoordType> vec)
{
Vector3D<CoordType> result;
result.x = x-vec.x;
result.y = y-vec.y;
result.z = z-vec.z;
return result;
}
Vector3D<CoordType> operator + (Vector3D<CoordType> vec)
{
Vector3D<CoordType> result;
result.x = x+vec.x;
result.y = y+vec.y;
result.z = z+vec.z;
return result;
}
Vector3D<CoordType> operator * (CoordType v)
{
Vector3D<CoordType> result;
result.x = x*v;
result.y = y*v;
result.z = z*v;
return result;
}
// trying to simulate an expensive collision-test here
// otherwise it would not require sqrt at all
// if( v1.abs() < v2.abs() ){ } is not efficient. Just simulating heavy work.
CoordType abs()
{
return std::sqrt(x*x+y*y+z*z);
}
};
template<typename CoordType>
struct PointCloud
{
Vector3D<CoordType> point[125];
PointCloud(CoordType x, CoordType y, CoordType z)
{
for(int i=0;i<125;i++)
{
point[i].x=x+i%5-2.5f;
point[i].y=y+(i/5)%5-2.5f;
point[i].z=z+i/25-2.5f;
}
}
};
template<typename CoordType>
bool pointCloudIntersection(PointCloud<CoordType>& cl1, PointCloud<CoordType>& cl2)
{
for(Vector3D<CoordType>& p:cl1.point)
{
for(Vector3D<CoordType>& p2:cl2.point)
{
if((p-p2).abs()<1.0f)
{
return true;
}
}
}
return false;
}
template<typename CoordType>
bool intersectDim(const CoordType minx, const CoordType maxx, const CoordType minx2, const CoordType maxx2)
{
return !((maxx < minx2) || (maxx2 < minx));
}
#include"Generator.h"
template<typename CoordType>
struct AABBofPointCloud: public FastColDetLib::IParticle<CoordType>
{
AABBofPointCloud(int idPrm, PointCloud<CoordType> * pCloudPrm)
{
id=idPrm;
pCloud = pCloudPrm;
xmin=pCloud->point[0].x;
ymin=pCloud->point[0].y;
zmin=pCloud->point[0].z;
xmax=pCloud->point[0].x;
ymax=pCloud->point[0].y;
zmax=pCloud->point[0].z;
for(int i=0;i<125;i++)
{
if(xmin>pCloud->point[i].x)
xmin=pCloud->point[i].x;
if(ymin>pCloud->point[i].y)
ymin=pCloud->point[i].y;
if(zmin>pCloud->point[i].z)
zmin=pCloud->point[i].z;
if(xmax<pCloud->point[i].x)
xmax=pCloud->point[i].x;
if(ymax<pCloud->point[i].y)
ymax=pCloud->point[i].y;
if(zmax<pCloud->point[i].z)
zmax=pCloud->point[i].z;
}
}
int id;
PointCloud<CoordType>* pCloud;
CoordType xmin;
CoordType ymin;
CoordType zmin;
CoordType xmax;
CoordType ymax;
CoordType zmax;
const CoordType getMaxX()const {return xmax;}
const CoordType getMaxY()const {return ymax;}
const CoordType getMaxZ()const {return zmax;}
const CoordType getMinX()const {return xmin;}
const CoordType getMinY()const {return ymin;}
const CoordType getMinZ()const {return zmin;}
const int getId()const {return id;}
};
#include "AdaptiveGridTree.h"
int main()
{
using cotype = float;
PointCloud<cotype> ico1(0,0,0);
// heating the CPU for benchmarking
for(int i=0;i<10000;i++)
{
PointCloud<cotype> ico2(0,0.1f,i*0.1f);
pointCloudIntersection(ico1,ico2);
}
const int N = 40004;
std::vector<PointCloud<cotype>> objects;
oofrng::Generator<64> gen;
for(int i=0;i<N-3;i++)
{
// this time X range is 0-1500 instead of 0-150
objects.push_back(
PointCloud<cotype>(
gen.generate1Float()*1500,gen.generate1Float()*150,gen.generate1Float()*150)
);
}
// the teapot in stadium problem
objects.push_back(PointCloud<cotype>(9000,9000,9000));
objects.push_back(PointCloud<cotype>(9001,9001,9001));
objects.push_back(PointCloud<cotype>(9002,9002,9002));
std::vector<AABBofPointCloud<cotype>> AABBs;
for(int i=0;i<N;i++)
{
AABBs.push_back(AABBofPointCloud<cotype>(i,&objects[i]));
}
AdaptiveGridTree<7> test(0,0,0,10005,10005,10005);
for(int i=0;i<100;i++)
{
size_t nano;
{
FastColDetLib::Bench bench(&nano);
test.clear();
test.addParticles(N,AABBs.data());
const auto coll = test.computeAllPairs();
std::cout<<"c="<<coll.size()<<std::endl;
}
std::cout<<"t="<<nano<<std::endl;
}
return 0;
}
output:
c=11990 t=18833176 c=11990 t=18373216 c=11990 t=18464937 c=11990 t=18453505
10% less performance than 60 FPS for nearly 12000 collisions.
The performance scaling problem is mainly caused by deduplication (that is bottlenecked by RAM bandwidth and mutex locking throughput) and partially caused by single-threaded construction of the load-balancer tree. A CPU with turbo-frequency can boost these serially-running parts to achieve better performance scaling with more threads and faster RAM can yield much better overall performance.
When CPU frequency is changed to 3.6 GHz,
c=11990 t=16230516 c=11990 t=16768193 c=11990
there is only 10-15% performance gain. RAM access / mutex locking throughput in deduplication is keeping scaling low.
When particles are clustered on multiple regions, the performance scaling grows due to less number of adaptive grids constructed and less number of deduplications are computed:
4 clusters (10k particles each)
By changing only the pointcloud initialization part, several clusters are created:
// cluster 1
for(int i=0;i<10000;i++)
{
objects.push_back(
PointCloud<cotype>(
gen.generate1Float()*150,5000+gen.generate1Float()*1500,gen.generate1Float()*150)
);
}
// cluster 2
for(int i=0;i<10000;i++)
{
objects.push_back(
PointCloud<cotype>(
gen.generate1Float()*150,gen.generate1Float()*150, 5000+gen.generate1Float()*1500)
);
}
// cluster 3
for(int i=0;i<10000;i++)
{
objects.push_back(
PointCloud<cotype>(
5000 + gen.generate1Float()*150,gen.generate1Float()*150, 5000+gen.generate1Float()*1500)
);
}
// cluster 4
for(int i=30000;i<N-3;i++)
{
objects.push_back(
PointCloud<cotype>(
gen.generate1Float()*1500,gen.generate1Float()*150,gen.generate1Float()*150)
);
}
// the teapot in stadium problem
objects.push_back(PointCloud<cotype>(9000,9000,9000));
objects.push_back(PointCloud<cotype>(9001,9001,9001));
objects.push_back(PointCloud<cotype>(9002,9002,9002));
result:
c=2998 t=16395008 c=2998 t=16848125 c=2998 t=16174032 c=2998 t=16507923 c=2998 t=15759892 c=2998 t=16646543 c=2998 t=15984087 c=2998 t=15312543
Better than 60 FPS (~16 ms per computation on average).
16 clusters (2500 particles each)
for(int j=0;j<16;j++)
for(int i=0;i<2500;i++)
{
objects.push_back(
PointCloud<cotype>(
(j%2)*5000 + gen.generate1Float()*150,
((j/2)%2)*5000 +gen.generate1Float()*150,
(j/4)*2500 +gen.generate1Float()*150)
);
}
result:
c=7190 t=13297025 c=7190 t=13186931 c=7190 t=14142431 c=7190 t=13259546 c=7190 t=14085992 c=7190 t=13298677 c=7190 t=12839448
At ~13 milliseconds per computation (that is 77 FPS), it is at least 15% faster. Having equal-sized clusters also helps on load-balancing but it is not visible when load-balancer tree is very deep.
The slowness of 64-cluster version (uniform random distribution with 1 tree-depth) comes from extra work on deduplication. The more clusters, the worse performance on deduplication but also the better load-balancing. For the test system, 16 clusters has best performance while uniform distribution has worst performance but sustains high collision scaling (performance dropping not as fast as number of collision-pairs increase).
Benchmarks at Goldbolt.org (Intel(R) Xeon(R) Platinum 8124M CPU @ 3.00GHz, compiler options = -std=c++2a -O3 -march=native -mavx512f -mavx512bw -ftree-vectorize -ffast-math -fno-math-errno -lpthread ):
16 clusters + 2 threads: 14.4 milliseconds
16 clusters + 4 threads: 8.3 milliseconds (https://godbolt.org/z/8TE4znzhE)
Benchmarks at paiza.io (Intel(R) Xeon(R) Platinum 8175M CPU @ 2.50GHz):
16 clusters + 2 threads: 10.8 milliseconds
16 clusters + 4 threads: 10.7 milliseconds
Using multiple threads on shared-servers has performance scaling complications. Using another thread increases chances of sharing same core with another client.
https://wandbox.org/ (Intel(R) Xeon(R) E-2286G CPU @ 4.00GHz (4 threads, 16 clusters)): 9.3 milliseconds
https://rextester.com (Intel(R) Xeon(R) Gold 5215 CPU @ 2.50GHz (4 threads, 16clusters)): 10.0 milliseconds
When number of collisions is increased to 181000 (from 7000) by increasing particle density per cluster, fx8150 with 7 threads requires 23 milliseconds while Xeon Gold 5215 with 4 threads completes computations in 19 milliseconds.
For algorithms that do not require merging results from all nodes, tree structure is good enough for balancing loads between multiple threads for unknown particle densities.
Points of Interest
It is fun to work with uniform grid as a spatial acceleration structure, optimizing it to suit more scenarios. Currently, it is not very well balanced on inserting / querying performance ratio. Since inserting is simple, it will be straightforward to add multi-threading support as a next update.
Next challenge (completed): compute 20k AABB all-pair collisions at 60FPS for a simple physics simulation of spherical objects.
Third challenge (completed): compute 40k AABB all-pair collision detection at 60FPS, preferably in single-thread of same CPU (2.1GHz FX8150 + 1 channel 1333MHz ddr3 RAM)
Fourth challenge: compute 80k AABB all-pair collision detection at 60 FPS, on GT1030 GPU.
All diagrams were made in this site: https://app.diagrams.net/.
All graphs were visualized in this site: https://app.datawrapper.de
History
- Friday, 18th March, 2022: Initial submission with barely-enough performance for performance constraint given at the beginning of the article
- Monday, 4th April, 2022: Sparse-linear adaptive grid of 4x4x4 child node setting is implemented and tested while completing the second challenge of 20k particles' all-pair collision test at 60 FPS. Tests for AVX2 and AVX512 added
- Saturday, 16th April, 2022: Multithreaded load-balanced version of adaptive grid is implemented in the form of "tree of adaptive grids" and benchmarked while completing the third challenge of 40k particles' all-pair collision test at 60FPS.