Searching for shared motif between strings in C
4.50/5 (2 votes)
In this article, i consider the problem of identifying motifs in the biological sequence data sets. To solve this task, i present a new algorithm for finding patterns that just use <String.h> library in C compiler and a new way to avoid using arrays search.
Introduction
In this article, i consider the problem of identifying motifs in the biological sequence data sets. To solve this task, i present a new algorithm for finding patterns that just use <String.h> library in C compiler and a new way to avoid using arrays search.
Background
Finding motifs or repeated patterns in data is of wide scientific interest with many applications in genomic and proteomic analysis. The motif search problem abstracts many important problems in analysis of sequence data, where motifs are, for instance, biologically important patterns. For example, elucidating motifs in DNA sequences is a critical first step in understanding biological processes as basic as the RNA transcription. There, the motifs can be used to identify promoters, the regions in DNA that facilitate the transcription. Finding motifs can be equally crucial for analyzing interactions between viruses and cells or identification of disease-linked patterns. Discovery of motifs in music sequences, text, or time series data is a fundamental, general means of summarizing, mining and understanding large volumes of data. (Read More)
There is many ways and new algorithms for this topic but purposely in this article i just use <String.h> library in C language and i avoid using array search to find shared motid sub-string of two strings. this can help to code alghoritm in 50 lines or even less and also can reduce the percentage of error (especially in C compiler).
Also it can be a charming challenge!
Using the code
As we want to avoid using arrays so we need to use <String.h> library so we can include it to our project.
#include <string.h>
now we must search an string in another string. let char "s1" to be our first string and "s2" our second string and now searching for longest shared motif of s2 in s1. for example if s1 = "ACGTACGT" and s2 = "AACCGGTATA" then the longest shared motif can be "CG".
To do such a thing, our first string (s1) must lose its first char in each round of loop and our second string (s2) (also it lose its first char in every rounds of another loop) must be searched in our first string (s1) by strcmp() function which available in <string.h>.
also notice we must use a secondary loop for each string to counting and going forward. (because we want search each char of s2 in each char of s1).
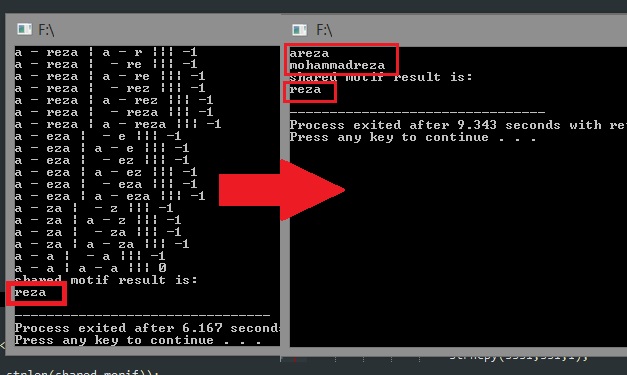
i use this peace of code for removing first char of each string to compare remaning string.
char *str = (char *)malloc(10); strcpy(str, s1); str = str + i;
and for better understanding i passed remaning strings to ss1 and sss1 which i define them at first (also for s2), and char shared_morif for final result.
//Defenition Area char s1[100], ss1[100], sss1[100]; char s2[100], ss2[100], sss2[100]; char shared_morif[100] = "";
now complete code:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
int main(int argc, char *argv[]) {
//Defenition Area
char s1[100], ss1[100], sss1[100];
char s2[100], ss2[100], sss2[100];
char shared_morif[100] = "";
int i,j,k,l,result, ls1, ls2;
scanf("%s", s1); scanf("%s", s2);
ls1 = strlen(s1); ls2 = strlen(s2);
//Main Algohritm
for (i=0; i<ls1; i++)
{
char *str = (char *)malloc(10);
strcpy(str, s1);
str = str + i;
strcpy(ss1, str);
for (j=0; j<ls2; j++)
{
char *str2 = (char *)malloc(10);
strcpy(str2, s2);
str2 = str2 + j;
strcpy(ss2, str2);
for (k=1; k<ls2 - j + 1; k++)
{
memset(sss2,0,strlen(sss2));
strncpy(sss2, ss2, k);
for (l=0; l<=strlen(ss1); l++)
{
memset(sss1,0,strlen(sss1));
strncpy(sss1,ss1,l);
result = strcmp(sss1,sss2);
//printf("%s - %s | %s - %s\n",ss1,ss2,sss1,sss2); //FOR TRACE & TEST
if (result == 0)
{
if (strlen(shared_morif) < strlen(sss2))
{
memset(shared_morif,0,strlen(shared_morif));
strcpy(shared_morif, sss2);
}
}
}
}
}
}
printf("shared motif result is:\n"); puts(shared_morif);
return 0;
}
note that in order to making strings null and clear i prefer to use memset() function.
memset(shared_morif,0,strlen(shared_morif));
at end i want mentioned to some notes when use string.h in c language:
- strcmp() returns 0 if the two strings are exactly the same.
- You cannot simply assign strings like (s1=("null") or sth like this) in C but you can use strcpy() for make string null.
