Add a point to a polyline
4.84/5 (7 votes)
Insert a new point to a polyline
- Download VB code - 30.8 KB
- Download VB code and demo - 62.8 KB
- Download C# code - 24.9 KB
- Download C# code and demo - 46.7 KB

Introduction
In many situations it is interesting to find the point closest to a line, and add a point in the line (like the dotted line in the picture above). There exists a formula for finding the distance from a point to a line like the one from MathWorld, but the problem with this is that it just finds the distance between an infinite extended line, based on two points on it, and a point. This means it would not be constrained by the limits of the line created by the surrounding lines.
The standard way of finding out which line to add the point to is the Voronoi diagram of line segment. The solution is very accurate, but it is not trivial to implement from scratch, even if you have a code for a normal Voronoi diagram of points. There are of course ready to use libraries, which you would have to pay to use, and not viable for use, and is in most cases (that I intend to use it for) a huge overkill. An example of such a Voronoi diagram could be seen below, were all the blue lines shows (for the most part) the boundary that is equally far form two lines:
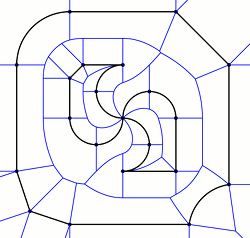
The algorithm that I will demonstrate would add the point if it is within the boundary of the blue line, meaning it would add the point to the closest line.
Background
There are several potential ways to solve this problem, one candidate would be to construct a Voroni diagram with lines, as described here, and this diagram would automatically set the boundaries for where the point should be added to the line. But unless you have a pre programmed code that is ready to use, this is quite a task. So I would like a simple solution to the problem.
One solution is to design an algorithm that takes the bend of the curve into consideration, and won't add the point to the line section if it is not within the boundaries. Boundaries are shown as red vectors in the picture below:

The Voroni diagram for a line would do this automatically.
Functions that are used
I must first describe some simple functions that is needed for the code to work. These are basic geometric functions that are used in several problems, and would be useful to have regardless of the problem at hand.
First we need to find the angel between two connected lines, and this could be done the "Law of cosine". The code below returns the angle in degrees.
''' <summary>
''' Calculate the angle in degrees between point 1 and 3 at point 2
''' </summary>
''' <param name="Point1"></param>
''' <param name="Point2"></param>
''' <param name="Point3"></param>
''' <returns></returns>
''' <remarks></remarks>
Public Function Angle(ByVal Point1 As Point, ByVal Point2 As Point, _
ByVal Point3 As Point) As Double
Dim result As Double
Dim a, b, c As Double
c = DistanceBetweenPoints(Point1, Point3)
b = DistanceBetweenPoints(Point1, Point2)
a = DistanceBetweenPoints(Point2, Point3)
result = Math.Acos((a ^ 2 + b ^ 2 - c ^ 2) / (2 * b * a)) * 180 / Math.PI
Return result
End Function
The next code snippet is the one from MathWorld that finds the distance from the point to the infinite line with two points through the line:
''' <summary>
''' Returns the distance from a point to a line
''' </summary>
''' <param name="LinePoint1"></param>
''' <param name="LinePoint2"></param>
''' <param name="TestPoint"></param>
''' <returns></returns>
''' <remarks></remarks>
Public Function DistanceFromLine(ByVal LinePoint1 As Point, _
ByVal LinePoint2 As Point, TestPoint As Point) As Double
Dim d As Double
d = Math.Abs((LinePoint2.X - LinePoint1.X) * (LinePoint1.Y - TestPoint.Y) - _
(LinePoint1.X - TestPoint.X) * (LinePoint2.Y - LinePoint1.Y))
d = d / Math.Sqrt((LinePoint2.X - LinePoint1.X) ^ 2 + (LinePoint2.Y - LinePoint1.Y) ^ 2)
Return d
End Function
The next issue is to find out which point the point is relative to the line, and this can be done by cross multiplication to find the normal vector to the line, and is explained here. The code looks like this:
''' <summary>
''' Finds which side of a line the point is
''' </summary>
''' <param name="PointToBeEvaluated">Evaluation point</param>
''' <param name="StartPointOnLine">Startpoint of line</param>
''' <param name="EndPointOnLine">Endpoint on line</param>
''' <returns>-1 for a point to the right, 0 for a point on the line, +1 for a point to the left</returns>
''' <remarks></remarks>
Private Function WhichSide(ByVal PointToBeEvaluated As Point, ByVal StartPointOnLine _
As Point, ByVal EndPointOnLine As Point) As Integer
Dim ReturnvalueEquation As Double
ReturnvalueEquation = ((PointToBeEvaluated.Y - StartPointOnLine.Y) _
* (EndPointOnLine.X - StartPointOnLine.X)) - ((EndPointOnLine.Y - StartPointOnLine.Y) _
* (PointToBeEvaluated.X - StartPointOnLine.X))
If ReturnvalueEquation > 0 Then
Return -1
ElseIf ReturnvalueEquation = 0 Then
Return 0
Else
Return 1
End If
End Function
One last function is needed for calculating the normal vector of a single line. This is nessesary for all the points.
''' <summary>
''' Calculates the Normal vector at point 1
''' </summary>
''' <param name="Point1"></param>
''' <param name="point2"></param>
''' <returns></returns>
''' <remarks></remarks>
Public Function Normal2D(ByVal Point1 As Point, ByVal point2 As Point) As Point
Dim p As New Point
Dim theta As Double
theta = Math.PI / 2
p.X = Math.Cos(theta) * (point2.X - Point1.X) - Math.Sin(theta) * (point2.Y - Point1.Y) + Point1.X
p.Y = Math.Sin(theta) * (point2.X - Point1.X) + Math.Cos(theta) * (point2.Y - Point1.Y) + Point1.Y
Return p
End Function
The code can now be constructed from these simple functions. We will start off by calculating all the boundary lines (shown in red in the first picture), and adding a vector that we could draw it in each point. The code is given below, an utilizes the functions above:
Public Function CalculateAllAngles(ByVal OriginalPointCollection As PointCollection) As List(Of VectorLine)
Dim result As New List(Of VectorLine)
For i As Integer = 0 To OriginalPointCollection.Count - 1
Dim NewVectorLine As New VectorLine
If i = 0 Then
NewVectorLine.Point2 = Normal2D(OriginalPointCollection(i), _
OriginalPointCollection(i + 1))
NewVectorLine.Point1 = OriginalPointCollection(i)
result.Add(NewVectorLine)
ElseIf i = OriginalPointCollection.Count - 1 Then
NewVectorLine.Point2 = Normal2D(OriginalPointCollection(i), _
OriginalPointCollection(i - 1), 3 * Math.PI / 2)
NewVectorLine.Point1 = OriginalPointCollection(i)
result.Add(NewVectorLine)
Else
NewVectorLine.Point1 = OriginalPointCollection(i)
Dim angl As Double = Angles(OriginalPointCollection(i - 1), _
OriginalPointCollection(i), OriginalPointCollection(i + 1))
Dim PreviousAngle, NextAngle As Integer
PreviousAngle = WhichSide(result(i - 1).Point2, _
OriginalPointCollection(i - 1), OriginalPointCollection(i))
NextAngle = WhichSide(OriginalPointCollection(i + 1), _
OriginalPointCollection(i - 1), OriginalPointCollection(i))
If PreviousAngle = NextAngle Then
NewVectorLine.Point2 = Normal2D(OriginalPointCollection(i), _
OriginalPointCollection(i + 1), angl / 2)
Else
NewVectorLine.Point2 = Normal2D(OriginalPointCollection(i), _
OriginalPointCollection(i + 1), (2 * Math.PI - angl) / 2)
End If
result.Add(NewVectorLine)
End If
Next
Return result
End Function
Public Class VectorLine
Public Point1 As New Point
Public Point2 As New Point
End Class
The code is rather simple, and could be broken into simple steps:
The first and the last point is calculated using, respectfully, the first and the last lines tilted at 90 and 270 degrees.
The angles of the other points are found by using the Law of cosine. The vector is calculated using the shortest angle, and if the calculated vector point is on the same side as the first calculated vector point it is stored. If its on the opposite side, the vector is recalculated by withdrawing the angle from the full circle.
The calculated vector lines then returned from the function.
The complete algorithm
The code that does the calculation is given below:
''' <summary>
''' Insert a new point to the line
''' </summary>
''' <param name="OriginalPointColletion"></param>
''' <param name="NewPoint"></param>
''' <returns></returns>
''' <remarks></remarks>
Public Function InsertPoint(ByVal OriginalPointColletion As PointCollection, _
ByVal NewPoint As Point) As PointCollection
Dim result As New PointCollection
result = OriginalPointColletion.Clone
Dim min_distance As Double = Double.MaxValue
'For Each p As Point In result
' min_distance += DistanceBetweenPoints(NewPoint, p)
'Next
Dim temp_distance As Double
Dim index As Integer
Dim VectorLinesCalc As New List(Of VectorLine)
VectorLinesCalc = CalculateAllAngles(OriginalPointColletion)
For i As Integer = 0 To OriginalPointColletion.Count - 2
temp_distance = DistanceFromLine2(NewPoint, VectorLinesCalc(i), VectorLinesCalc(i + 1))
If temp_distance < min_distance Then
min_distance = temp_distance
index = i + 1
End If
Next
If DistanceBetweenPoints(OriginalPointColletion(0), NewPoint) < min_distance Then
min_distance = DistanceBetweenPoints(OriginalPointColletion(0), NewPoint)
index = 0
End If
If DistanceBetweenPoints(OriginalPointColletion(OriginalPointColletion.Count - 1), NewPoint) < min_distance Then
index = -1
min_distance = DistanceBetweenPoints(OriginalPointColletion(OriginalPointColletion.Count - 1), NewPoint)
End If
If Not index = -1 Then
result.Insert(index, NewPoint)
Else
result.Add(NewPoint)
End If
Return result
End Function
I simply calculate the distance from each line to the new point you are trying to intersect. However if the point is not within the boundaries the distance Double.MaxValue
is returned. This would guarantee that the point with the shortest distance is natural closest to the line in question.
The way I find out if the points are outside the boundary is to check whether the two boundary vectors are not equal to each other, since we are evaluating the calculations on the distance this would work fine.
History
The code has massively been upgraded due to a bug. In addition the UI has also been upgraded, mostly in order to bug check the code, but it should also help you understand the algorithm in more detail. Code is given in C# and VB and the main function is also encapsulated in a own class/module so it could easily be implemented for others.
