HTTree - Hacked Ternary Tree Implementation
This is a new type of tree based on the ternary tree algorithm
Introduction
This project is to show the tree I dreamed of when I first met the ternary tree concept. When I came upon the ternary tree, I get awed! It's amazing that an idea so simplistic could be so strong and fast. But it had flaws... the first one is the memory consumption. The hash table implementation consumes far less memory than the ternary tree! The second flaw is the ternary tree can be fragmented and be extremely unbalanced (as the algorithm doesn't do any balancing step) so the tree also needs a way for balancing the nodes. I tried to reduce the memory consumption by grouping three nodes into one new "int" node.
Sorry, but this tree is still "unbalanced". ;-)
From Where It Came...
The normal ternary tree node (one node and the three "near" nodes):
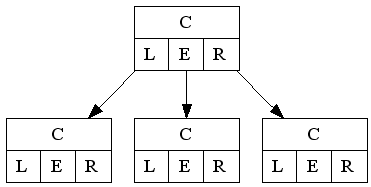
C language representation:
struct TTNode{
char C;
TTNode *Left,*Equal,*Right;
};
One char "C" (key for this node and this position) and three pointers to follow when comparing ( "L"eft, "E"qual and "R"ight).
If the char you seek is equal to the char stored in C, then go to node pointed by Equal and continue... if it's less than char stored in C, go to Left or else, go to Right! (This is the ternary tree concept.)
The new hacked ternary tree node:

C language representation:
struct HTNode{
int C;//(M,N,L and R characters)
Node *LL,*LE,*LR,*EL,*EE,*ER,*RL,*RE,*RR;
//or LeftLeft,LeftEqual,LeftRight,EqualLeft,EqualEqual,
//EqualRight,RightLeft,RightEqual,RightRight;
};
Now the thing gets a lot complicated! Other than three pointers, we have nine pointers! and the C character is now four chars inside one int! (M for mine, N for next, L for left and R for right)
The new node is a "merge" of ones from the previous image. The pointers each one had are now part of the new HTTNode.
Well now you may guess: "but what's the point this guy is doing? Where can this use less memory than the last one?? I think he's crazy..."
Now the secret: the char type is one byte, right? But the memory is taken int by int! So even if you use one char at a time, the memory is using an int size for storing this char!!!
Now see, I grouped the M, N , L and R chars in one int and put aside the ptr Left, ptr Equal and ptr Right (as the Next, Left and Right are also in the node). With this, I managed to strip off 6 ints from my tree node!
Now another question may arise: "but now the node is bigger! Can the memory usage be less than using the first tree node?? It's faster?"
The answer is: "yes, it can be bigger, but using the tree for words, names or numbers we get a lot of 'pairs' with same M and N (even if you insert in an 'unbalanced' way). This tree test for this type of occurrence to do a faster insertion and faster search than the previous one (by comparing a word instead of a byte)".
I'm leaving the code and algorithm as open source as I think this is something everybody must have free access to use and modify in any way.
Now the algorithm for the insertion (the search is 90% equal, just return "found" instead of storing a value...).
LRNM = how the int stores the four characters ( Left, Right, Next and Mine)
DCBA = int "view" of a char array (as the system is big endian)
[] = condition to test
S means condition returned true
(from the word "Sim" meaning "yes" in Portuguese ;-)
N means condition returned false (from "No")
== = test for equality
= = assignment
> = test for "more than"
+# = plus number => increment the string we are searching
by the number and pass it to the function
collision = the value is already there for this key.
The indentation is also for showing "branching" for the algorithm.
(as python this algorithm uses
indentation to group statements for a given condition).
LRNM DCBA
[A == 0]
S return error!
[NODE == NULL]
S return error! (should never happen if you did everything right)
[MN == 00]
S [B == 0]
S M = A
insert value
return r;
N MN = AB
[C == 0]
S inset nvalue
return r;
N insert EE +2
N [B == 0]
S [M == 0]
S M = A
insert value
return r;
N [M == A ]
S return collision!
N [ M > A]
S [L == 0]
S L = A
insert lvalue
N [L == A]
S return collision
N [L > A]
S insert LL +0
N insert LR +0
N [R == 0]
S R = A
insert rvalue
N [R == A]
S return collision
N [R > A]
S insert RL +0
N insert RR +0
N [NM == BA]
S [C == 0]
S insert nvalue
return r
N insert EE +2
N [M == 0]
S M = A
insert value
return r;
N [M == A ]
S [N == 0]
S [C == 0]
S insert nvalue return r;
N [ N == B]
S [C == 0]
S return collision
N insert EE +2
N [N > B]
S insert EL +1
N insert ER +1
N [ M > A]
S [L == 0]
S L = A
insert lvalue
N [L == A]
S insert LE +1
N [L > A]
S insert LL +0
N insert LR +0
N [R == 0]
S R = A
insert rvalue
N [R == A]
S insert RE +1
N [R > A]
S insert RL +0
N insert RR +0
About the Demo Code
The demo code for this project is the HTTree implementation inside a console project with two tests, one test showing the normal usage of the tree and another using a normal ternary tree to test the data integrity of the new tree.
Both had huge memory usage and if you have less than one gigabyte of RAM memory, you should change the internal values to avoid hitting the swap file...
I know that the bit shift stuff could be a little strange, but it was easier to me to do things with them. Feel free to use the algorithm description to build your own version of the tree in the language you like to use! ;-)
Final Considerations
I'm planning to also put a speed and memory test for this tree (I already have the speed test and it is faster than the normal ternary tree) and when I finish it, I'll post it too.
I hope you enjoy it as I did creating it... ;-) . If you enjoy-it feel free to send comments!
I also ask for suggestions for a name for this new tree as it is a lot different from the original ternary tree. I called it "hacked", but I think we can get another (better) name.
History
- 6th June, 2006: Initial post
