Optimizing Linear Regression Method with Intel® Data Analytics Acceleration Library
This article describes a common type of regression analysis called linear regression and how the Intel® Data Analytics Acceleration Library (Intel® DAAL) helps optimize this algorithm when running it on systems equipped with Intel® Xeon® processors.
How does a company forecast how much it can spend on future advertising in order to increase sales? Similarly, how much should a company spend in future training programs in order to improve productivities?
In both cases, those companies rely on the historical relationship between variables like, in the former case, the relationship between the sale value and advertising spending to predict the future outcome.
This is a typical regression problem that can be best solved using machine learning1.
This article describes a common type of regression analysis called linear regression2 and how the Intel® Data Analytics Acceleration Library (Intel® DAAL)3 helps optimize this algorithm when running it on systems equipped with Intel® Xeon® processors.
What is Linear Regression?
Linear regression (LR) is the most basic type of regression that is used for predictive analysis. LR shows a linear relationship between variables and how one variable can be affected by one or more variables. The variable which is impacted by the others is called a dependent, response, or outcome variable and the others are called independent, explanatory, or predictor variables.
In order to use LR analysis, we need to examine whether LR is suitable for this set of data. To do that we need to observe how the data is distributed. Let's look at the following two graphs:


In figure 1, we can fit a straight line through the data points; however, there is no way to do that with the data points in figure 2. Only the curved (non-linear) line can be fitted through the data points in figure 2. Therefore, linear regression analysis can be done on the dataset in figure 1, but not on that in figure 2.
Depending on the number of independent variables, LR is divided into two types: simple linear regression (SLR) and multiple linear regression (MLR).
LR is called SLR when there exists only one independent variable, whereas MLR has more than one independent variable.
The simplest form of the equation with one dependent and one independent variable is defined as:
y = Ax + B (1)
Where:
y: Dependent variable
x: Independent variable
A: Regression coefficient or slope of the line
B: Constant
The question is how to find the best-fit line so that the difference between the observed and predicted values of the dependent variable (y) is minimum. In other words, find A and B in equation (1) such that |yobserved – ypredicted| is minimum.
The task to find the best-fit line can be done using the least squares method4. It calculates the best-fit line by minimizing the sum of the squares of the vertical differences (difference between the observed and predicted values of y) from each data point to the line. The vertical difference can also be called residual.
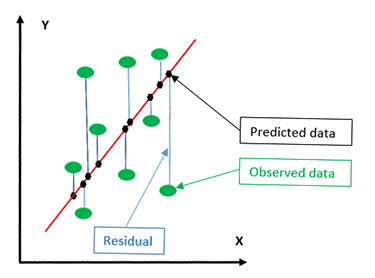
From figure 3 the green dots represent the actual data points. The black dots show the vertical (not perpendicular) projection of the data points onto the regression line (red line). The black dots are also called the predicted data. The vertical difference between the actual data and the predicted data is called residual.
Applications of Linear Regression
Some of the applications that can make good use of linear regression:
- Forecasting future sales.
- Analyzing the marketing effectiveness and pricing on sales of a product.
- Assessing risk in financial services or insurance domains.
- Studying engine performance from test data in automobiles.
Advantages and Disadvantages of Linear Regression
Some of the pros and cons of LR:
- Advantages
- The result is optimum when the relationship between the independent and the dependent variables are almost linear.
- Disadvantages
- LR is very sensitive to outliers.
- It is inappropriately used to model non-linear relationships.
- Linear regression is limited to predicting numeric output.
Intel® Data Analytics Acceleration Library
Intel DAAL is a library consisting of many basic building blocks that are optimized for data analytics and machine learning. These basic building blocks are highly optimized for the latest features of the latest Intel® processors. LR is one of the predictive algorithms that Intel DAAL provides. In this article, we use the Python* API of Intel DAAL to build a basic LR predictor. To install DAAL, follow the instructions in How to install the Python Version of Intel DAAL in Linux*5.
Using Linear Regression Algorithm in Intel Data Analytics Acceleration Library
This section shows how to invoke the linear regression method in Python6 using Intel DAAL.
The reference section provides a link7 to the free datasets that can be used to test the application.
Do the following steps to invoke the algorithm from Intel DAAL:
- Import the necessary packages using the commands from and import.
- Import Numpy by issuing the command:
import numpy as np
- Import the Intel DAAL numeric table by issuing the following command:
from daal.data_management import HomogenNumericTable
- Import necessary functions to numeric tables to store data:
from daal.data_management import ( DataSourceIface, FileDataSource, HomogenNumericTable, MergeNumericTable, NumericTableIface)
- Import the LR algorithm using the following commands:
from daal.algorithms.linear_regression import training, prediction
- Import Numpy by issuing the command:
- Initialize the file data source if the data input is from the .csv file:
trainDataSet = FileDataSource( trainDatasetFileName, DataSourceIface.notAllocateNumericTable, DataSourceIface.doDictionaryFromContext ) - Create numeric tables for training data and dependent variables:
trainInput = HomogenNumericTable(nIndependentVar, 0, NumericTableIface.notAllocate) trainDependentVariables = HomogenNumericTable(nDependentVariables, 0, NumericTableIface.notAllocate) mergedData = MergedNumericTable(trainData, trainDependentVariables)
- Loading input data:
trainDataSet.loadDataBlock(mergedData)
- Create a function to train the model.
- First create an algorithm object to train the model using the following command:
algorithm = training.Batch_Float64NormEqDense()
Note: This algorithm uses the normal equation to solve the linear least squares problem. DAAL also supports QR decomposition/factorization. - Pass the training dataset and dependent variables to the algorithm using the following commands:
algorithm.input.set(training.data, trainInput) algorithm.input.set(training.dependentVariables, trainDependentVariables)
where
algorithm: The algorithm object as defined in step a above. train
Input: Training data. trainDependent
Variables: Training dependent variables - Train the model using the following command:
trainResult = algorithm.compute()
where
algorithm: The algorithm object as defined in step a above.
- First create an algorithm object to train the model using the following command:
- Create a function to test the model.
- Similar to steps 2, 3, and 4 above, we need to create the test dataset for testing:
i.testDataSet = FileDataSource( testDatasetFileName, DataSourceIface.doAllocateNumericTable, DataSourceIface.doDictionaryFromContext )
ii.testInput = HomogenNumericTable(nIndependentVar, 0, NumericTableIface.notAllocate) testTruthValues = HomogenNumericTable(nDependentVariables, 0, NumericTableIface.notAllocate) mergedData = MergedNumericTable(testDataSet, testTruthValues)
iii.testDataSet.loadDataBlock(mergedData)
- Create an algorithm object to test/predict the model using the following command:
algorithm = prediction.Batch()
- Pass the testing data and the train model to the model using the following commands:
algorithm.input.setTable(prediction.data, testInput) algorithm.input.setModel(prediction.model, trainResult.get(training.model))
where
algorithm: The algorithm object as defined in step a above.
testInput: Testing data. - Test/predict the model using the following command:
Prediction = algorithm.compute()
- Similar to steps 2, 3, and 4 above, we need to create the test dataset for testing:
Conclusion
Linear regression is a very common predictive algorithm. Intel DAAL optimized the linear regression algorithm. By using Intel DAAL, developers can take advantage of new features in future generations of Intel Xeon processors without having to modify their applications. They only need to link their applications to the latest version of Intel DAAL.
