Coding Challenge: Smallest Circle Problem
4.86/5 (20 votes)
Think algorithm...
Introduction
Most of us at most of the time doing computations using ready-made libraries/functions, that already implement the best algorithm to solve our problem. It is a few who do the mathematical brain-exercise and create algorithms for new problems or situations. Exactly that we will do now… Build an algorithm without looking up in our favorite search engine, using only our very own brain and some basic math.
The problem of the smallest circle surrounding all points in set is an old (around 150 years) mathematical problem, but nevertheless has no perfect solution… In search of a fast solution different people created different algorithms, with varying execution time, like O(n<sup>4</sup>), O(h<sup>3</sup>n), O(n log n) and finally - about 30 years ago - O(n).
In this article we will create an algorithm of O(n), probably one of the fastest possible...
Using the code
The code samples in the article are from the attached code and can not execute as is - you need the supporting code for input and output... For the complete solution download the attached project, created with VS Code and .NET Core (so you can use Linux or Mac too).
Basics
It is an old debate, if developers have to know math or not, and if do, to what extent. However for this specific problem you HAVE to know some basics, to understand me without proper mathematical proof (yes I will NOT go into detailed mathematical proof of everything, as it may take a book).
For make it simple we assume some:
- There is at least three points in the set
- Never any three of the points will form a line
You have to know/understand that
- Three points (a triangle) defines exactly one circle
- A circle defined by its center and radius, so points ON the circle are considered to be IN
- You have to understand simple vector computations, like distance between two points, intersection of two vectors… (or at least take my word for the formulas)
Special Cases
These are the cases when there are less than four points in the set. For those cases there is an exact solution for each case
- One point: The point itself the center and radius is zero
- Two points: The center is the middle of the vector and radius is the half of the length of the vector
- Three points: Form a triangle and the solution is the circumcircle (one that passes all three points)
- Three points that form a line: It is like the two point option, after we drop the middle point
While there are solutions for all these cases, I do not want to include them in the code as I want to focus on the development of our main algorithm...
Look At The Problem
The most interesting part of this problem is, that it is very easily solved by humans, looking at the set only. However computers do not look and do not see. For the instance look at the set below, give yourself a few moments and you will see which are the significant points that define the surrounding circle.

The Most Straightforward Solution - Brute Force
The basic idea is to run over the points in the set and extend the initial circle to include them. The starting circle is made from the first three points of the set (the circumcircle), so the actual running is starting from the fourth point…
So at every step, we have a circle, created from the triangle of the previous step and a new point. The idea is to replace the closest point to the new one with the new one and recompute the circumcircle… This approach is perfectly linear, as we hit every point only once, so the execution time depends only on the number of points in the set.
Let see the main part of the code:
public static Circle BruteForce(Set Set)
{
Circle oCircle = new Circle();
oCircle.Init(Set[0], Set[1], Set[2]);
for (int nIndx = 3; nIndx < Set.Count; nIndx++)
{
Point oNew = Set[nIndx];
double nD = Math.Sqrt(Math.Pow(oCircle.O.X - oNew.X, 2) + Math.Pow(oCircle.O.Y - oNew.Y, 2));
Dictionary<double, Point> oSel = new Dictionary<double, Point>();
if (nD > oCircle.R)
{
oSel.Add(Math.Sqrt(Math.Pow(oCircle.A.X - oNew.X, 2) + Math.Pow(oCircle.A.Y - oNew.Y, 2)), oCircle.A);
oSel.Add(Math.Sqrt(Math.Pow(oCircle.B.X - oNew.X, 2) + Math.Pow(oCircle.B.Y - oNew.Y, 2)), oCircle.B);
oSel.Add(Math.Sqrt(Math.Pow(oCircle.C.X - oNew.X, 2) + Math.Pow(oCircle.C.Y - oNew.Y, 2)), oCircle.C);
List<double> oList = oSel.Keys.ToList();
oList.Sort();
oSel[oList[0]] = oNew;
oCircle = new Circle();
oCircle.Init(oSel[oList[0]], oSel[oList[1]], oSel[oList[2]]);
}
}
return (oCircle);
}
The circle created from three points (via the Init method). I use the distance of each of the three from the new point as an index to pick the one to replace and recompute the circle. I skip points already inside the current circle...
Let see the result:

D and the blue after adding E.
F skipped, because it is already inside after adding E.
Now that’s a good, solid solution, with only one problem - not always gives the right answer…
Let see another set with its result:

D skipped as already in, but when adding E all goes wrong...
The circle (the green arc) is far too large, and D is outside of it...
By looking at the result, one could come to the conclusion, the instead of replacing the closest point to create the new circle, we should create the two possible circles (we are not using the most far point of the reason, that it will only mirror the circle instead of extending it) and choose the smallest.
Here the code for this version of brute-forcing:
public static Circle BruteForce2(Set Set)
{
Circle oCircle = new Circle();
oCircle.Init(Set[0], Set[1], Set[2]);
for (int nIndx = 3; nIndx < Set.Count; nIndx++)
{
Point oNew = Set[nIndx];
double nD = Math.Sqrt(Math.Pow(oCircle.O.X - oNew.X, 2) + Math.Pow(oCircle.O.Y - oNew.Y, 2));
Dictionary<double, Point> oSel = new Dictionary<double, Point>();
if (nD > oCircle.R)
{
oSel.Add(Math.Sqrt(Math.Pow(oCircle.A.X - oNew.X, 2) + Math.Pow(oCircle.A.Y - oNew.Y, 2)), oCircle.A);
oSel.Add(Math.Sqrt(Math.Pow(oCircle.B.X - oNew.X, 2) + Math.Pow(oCircle.B.Y - oNew.Y, 2)), oCircle.B);
oSel.Add(Math.Sqrt(Math.Pow(oCircle.C.X - oNew.X, 2) + Math.Pow(oCircle.C.Y - oNew.Y, 2)), oCircle.C);
List<double> oList = oSel.Keys.ToList();
oList.Sort();
Circle oC1 = new Circle();
oC1.Init(oSel[oList[0]], oNew, oSel[oList[2]]);
Circle oC2 = new Circle();
oC2.Init(oNew, oSel[oList[1]], oSel[oList[2]]);
oCircle = oC1.R < oC2.R ? oC1 : oC2;
}
}
return (oCircle);
}
But looking at the next sample set, we can see that it’s no good either…
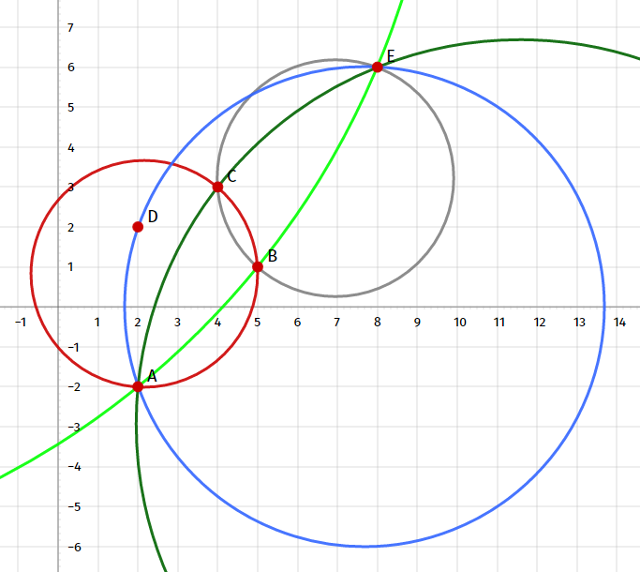
D was skipped as it is inside already.
We compared circle ACE (dark green arc) and ABE (light green arc) and found ACE to be the smaller, however the true solution is the blue circle.
So far - using pure intuitions and simple logic - we got nowhere, time to include some more...
Toward The True Solution
After a while working with computers we used to see problems as a machine and break it apart to make it comfortable to the machine. In some cases - like this one - it just does not works out as expected... So I invite you to rethink our approach...
Stop for a moment and try to recall how you solved the first sample I gave you (when asked you to see and solve). I for one solved it by elimination the innermost points of the set and concentrating only on those on the perimeters. Working with only those gave me an instant solution...
For that, I conclude, that we should not use all the point in the set to find the smallest circle, but only those are on the perimeters of the set. It is easy to understand that those points are in the central area of the set do not play a real part in the final result, while those on the perimeters are the important ones.
To find the points on the perimeters I introduce a new problem (do not panic - it has a most simple solution): The smallest rectangle surrounding all points.
To determine the rectangle, all we need is to scan the set and find the maximum and minimum of the X and Y coordinates of the points.
Now, it is easy to see and understand that a circle crossing all four edge points of that rectangle surrounding all the points of the set too, So all those points inside the smallest rectangle will also be inside the smallest circle, while those are on the smallest rectangle, either will be on or inside the smallest circle.
However this is not necessarily the smallest circle, as - depending on the position of the points on the rectangle, some of them may be on the circle and not inside it…

So this solution has two steps:
- Remove all the irrelevant points from the set
- Run a simple brute force on the rest
And here the code:
public static Circle BruteForceFixed(Set Set)
{
Set oSet = new Set();
oSet.AddRange(Set);
oSet.RemoveAll(oPoint =>
(oPoint.X < oSet.Max(oTemp => oTemp.X)) &&
(oPoint.X > oSet.Min(oTemp => oTemp.X)) &&
(oPoint.Y < oSet.Max(oTemp => oTemp.Y)) &&
(oPoint.Y > oSet.Min(oTemp => oTemp.Y)));
List<Point> oEdges = oSet.FindAll(oPoint =>
((oPoint.X == oSet.Max(oTemp => oTemp.X)) && (oPoint.Y == oSet.Max(oTemp => oTemp.Y))) ||
((oPoint.X == oSet.Max(oTemp => oTemp.X)) && (oPoint.Y == oSet.Min(oTemp => oTemp.Y))) ||
((oPoint.X == oSet.Min(oTemp => oTemp.X)) && (oPoint.Y == oSet.Max(oTemp => oTemp.Y))) ||
((oPoint.X == oSet.Min(oTemp => oTemp.X)) && (oPoint.Y == oSet.Min(oTemp => oTemp.Y)))
);
if(oEdges.Count >= 2)
{
oSet.Clear();
oSet.AddRange(oEdges);
}
if (oSet.Count == 2)
{
oSet.Add(new Point() { X = oSet[0].X, Y = oSet[1].Y });
}
return (BruteForce(oSet));
}
This code handles the special case, you probably already asked about... The smallest rectangle declared by two edge points only... That of course will lead to one of our special cases we mentioned before, and to overcome it I add a third - fictional - point to the set, a third edge point...
I also take in account the case when there are at least two edge points of the smallest rectangle in the set - in this case all the other points are irrelevant and running the brute force on them will give the wrong answer...
But behold! Event this solution will not save us. See this set:

H is outside the blue!
The End
Make asummary of what we have learned so far:
- A simple run on the poinst will not work every set
- Identifying the smallest rectangle helps for sure only in cases where the points on the perimeters are actualy define that rectanle (meaning that at least two of them are edge poinst)
From all these we can identify two cases:
- The smallest circle defined by two points only
- The smallest circle defined by three points exactly
We already identified some cases for each, but always found loopholes. However looking at the last set and the one below we can spot something very important.

D is outside of it!
From these images we can conveive a definiton that can help us deside when to use two, and when three, of the points on the perimeter of the set.
One conclusion is, that the points will come from the set of three points found most far from the center of the smallest rectange. To see if we will use all three or only two of them we have to check the distance between every pair of them. What we looking for is the longest of those distances to check if it is large enought ot be the diameter of the circle... If it is than we need only these two points to declare the circle, otherwise we need all three.
How we now it is larger enough? If the distance of the third point from the sencter smaller than the half of that distance, even the third point is inside the smallest circle... Let see it on some drawing:

A, B and C are the points, most far from the rectangle's center. However the distance of B is less then the half of the distance bwtween A and C (the largest in this trio), so the circle defined by A and C only!

E, F and H are the points, most far from the rectangle's center. The distance of E is larger then the half of the distance bwtween F and H (the largest in this trio), so the circle defined by E, F and H too!
So the solution goes like this:
- Find the center point of the smallest rectangle
- Find the three points most far from that center
- If there are two points on the edges of the smallest rectangle, those two point define the smallest circle too
- If there is one point on the edges of the smallest computer we have our three points to define the circle
- Otherwise check the longest side of that triangle against the distance of the third point to see how many points define the smallest circle
- Compute the circle
The code for all this combined:
public static Circle BruteForceFinal(Set Set)
{
Set oSet = new Set();
Circle oCircle = new Circle();
Point oO = new Point()
{
X = ((Set.Max(oPoint => oPoint.X) + Set.Min(oPoint => oPoint.X)) / 2),
Y = ((Set.Max(oPoint => oPoint.Y) + Set.Min(oPoint => oPoint.Y)) / 2)
};
oSet.AddRange(Set.OrderByDescending(oPoint => Math.Sqrt(Math.Pow(oPoint.X - oO.X, 2) + Math.Pow(oPoint.Y - oO.Y, 2))).Take(3));
List<Point> oEdges = oSet.FindAll(oPoint =>
((oPoint.X == Set.Max(oItem => oItem.X)) && (oPoint.Y == Set.Max(oItem => oItem.Y))) ||
((oPoint.X == Set.Max(oItem => oItem.X)) && (oPoint.Y == Set.Min(oItem => oItem.Y))) ||
((oPoint.X == Set.Min(oItem => oItem.X)) && (oPoint.Y == Set.Max(oItem => oItem.Y))) ||
((oPoint.X == Set.Min(oItem => oItem.X)) && (oPoint.Y == Set.Min(oItem => oItem.Y)))
);
Console.Write("Edges: ");
foreach (Point oPoint in oEdges)
{
Console.Write(string.Format("({0}, {1})", oPoint.X, oPoint.Y));
}
Console.WriteLine();
if (oEdges.Count == 2)
{
oSet.Clear();
oSet.AddRange(oEdges);
}
else if (oEdges.Count == 0)
{
Dictionary<double, Point> oTemp = new Dictionary<double, Point>();
oTemp.Add(D(oSet[0], oSet[1]), oSet[2]);
oTemp.Add(D(oSet[0], oSet[2]), oSet[1]);
oTemp.Add(D(oSet[1], oSet[2]), oSet[0]);
KeyValuePair<double, Point> oLarge = oTemp.OrderByDescending(oItem => oItem.Key).First();
if (oLarge.Key > D(oLarge.Value, oO))
{
oSet.Remove(oLarge.Value);
}
}
if (oSet.Count == 2)
{
oSet.Add(new Point() { X = oSet[0].X, Y = oSet[1].Y });
}
oCircle.Init(oSet[0], oSet[1], oSet[2]);
return (oCircle);
}
And that is the final word...
Summary
I did not spend much time to share mathematical proofs for my statements, neither explaining the rather complicated code to compute the intersection of two lines (you can see it in the attached code only), and that because my point is more to make you realize, that a good algorithm involves mixing the machine-like thinking with the human thinking.
Last Bits
If you are in doubt about the O(n) nature of the final solution, think about this: O(n) means, that the only factor changes the execution time is the number of the elements we iterate thru. So even we have two or more passes, we hit once every element in every pass, so we are still O(n).
And a word about the images. If you ever in need to create such images, search for 'scetchometry'. It is free and awesome...
