Introduction
This article helps the beginner of an AI course to learn the objective and implementation of Uninformed Search Strategies (Blind Search) which use only information available in the problem definition.
Uninformed Search includes the following algorithms:
- Breadth First Search (BFS)
- Uniform Cost Search (UCS)
- Depth First Search (DFS)
- Depth Limited Search (DLS)
- Iterative Deepening Search (IDS)
- Bidirectional Search (BS)
Background
This article covers several Search strategies that come under the heading of Uninformed Search. The term means that the strategies have no additional information about States beyond that provided in the problem definition. All they can do is generate successors and distinguish a goal state from a non-goal state. All Search strategies are distinguished by the order in which nodes are expanded.
To go ahead in these series, I will use some AI terminologies such as the following:
A problem can be defined by four components:
- Initial State that the problem starts in
- Goal State that the problem ends in
- Finding sequences of actions that lead to Goal State
- A path Cost to solve problem
Together, the initial state, goal state, actions and path cost define the state space of the problem (the set of all states reachable from the initial state by any sequence of actions). The path in the state space is a sequence of states connected by a sequence of actions. A solution to the problem is an action sequence that leads from the initial state to the goal state.
The process of looking at a sequence of actions that reaches the goal is called search. A search algorithm takes a problem as input and returns a solution in the form of an action sequences. The search starts from the initial state which represents the root node in the problem search space. The branches are actions and the nodes corresponding to the states in the problem state space.
Example
A small part of the 8-puzzle problem state space:
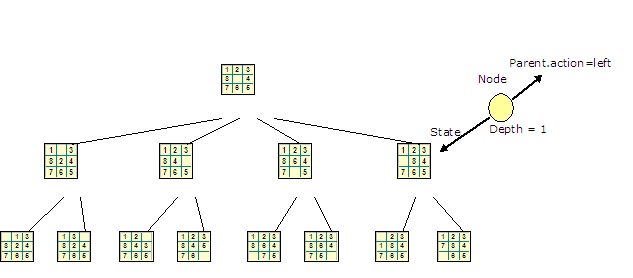
Note: Depth=number of steps from initial state to this state.
A collection of nodes that are generated but not yet expanded is called the fringe; each element of fringe is a leaf node (i.e. with no successors in tree).
Let's start to explain the first two algorithms of blind search:
- Breadth First Search (BFS): is a simple strategy in which the root node is expanded first, then all the successors of the root node are expanded next, then their successors, and so on. Fringe is a FIFO queue.
- Uniform Cost Search (UCS): modifies BFS by always expanding the lowest cost node on the fringe using path cost function g(n) (i.e. the cost of the path from the initial state to the node n). Nodes maintained on queue in order of increasing path cost.
- Depth First Search (DFS): always expands the deepest node in the current fringe of the search tree. Fringe is a LIFO queue (Stack).
- Depth Limited Search (DLS): The embarrassing failure of DFS in infinite state spaces can be alleviated by supplying DFS with a predetermined depth limit l, that is nodes at depth l are treated as if they have no successors.
- Iterative Deepening Depth First Search (IDS): is a general strategy often used in combination with depth first tree search that finds the best depth limit. It does this by gradually increasing limit first 0, then 1, then 2, and so on until the goal is found.
- Bidirectional Search (BS): The idea behind bidirectional search is to simultaneously search both forward from the initial state and backward from the goal state, and stop when the two searches meet in the middle. Here there are two fringes, one that maintains nodes forward and other that maintains nodes backward. Each fringe is implemented as LIFO or FIFO depends on the search strategy used in the search (i.e. Forward=BFS, Backward=DFS).
Using the Code
The first class in my code is Node.cs which represents the node as a data structure in the state space. Each node has some attributes such as depth, cost, state, and parent node. The state attribute is defined according to a physical configuration within the problem state space. My code is simply searching for a number in the state space of positive numbers so the state here is defined simply as an integer number.
Let's explore the Node class by the following snippet:
class Node
{
public int depth;
public int State;
public int Cost;
public Node Parent;
public Node (int State)
{
this.State = State;
this.Parent = null;
this.depth = 0;
}
public Node(int State)
{
this.State = State;
}
public Node(int State,Node Parent)
{
this.State = State;
this.Parent = Parent;
if (Parent == null)
this.depth = 0;
else
this.depth = Parent.depth + 1;
}
public Node(int State, Node Parent, int Cost)
{
this.State = State;
this.Parent = Parent;
this.Cost = Cost;
if (Parent == null)
this.depth = 0;
else
this.depth = Parent.depth + 1;
}
}
My code search is for a number in the range from 0, 1, 2, .N. so, the initial state is 0 and the goal state is the number specified
by the user. Each step of number generation costs random number or 1. Class GetSucc.cs defines GetSussessor() function
which includes the possible set of actions that are required for positive number generation in order. The input of GetSussessor() is the current state of the problem (i.e. initial State 0) and the output is the ArrayList of next states that are reached from current state(i.e. from 0 the next states 1,2 assuming that our tree is the binary tree).

class GetSucc
{
public ArrayList GetSussessor(int State)
{
ArrayList Result = new ArrayList();
Result.Add(2 * State + 1);
Result.Add(2 * State + 2);
return Result;
}
public ArrayList GetSussessor_Reverse(int State)
{
ArrayList Result = new ArrayList();
if (State % 2 == 0)
{
int P = State / 2 - 1;
Result.Add(P);
}
else
{
int Sib = State + 1;
Result.Add(Sib / 2 - 1);
}
return Result;
}
public ArrayList GetSussessor(int State,Node Parent)
{
ArrayList Result = new ArrayList();
Random n = new Random();
Test s = new Test();
Result.Add(new Node(2* State + 1,Parent,n.Next(1,100)+Parent.Cost));
Result.Add(new Node(2* State + 2, Parent,n.Next(1,100) + Parent.Cost));
Result.Sort(s);
return Result;
}
}
public class Test : IComparer
{
public int Compare(object x, object y)
{
int val1 = ((Node)x).Cost;
int val2 = ((Node)y).Cost;
if (val1 <= val2)
return 1;
else
return 0;
}
}
From here, let's begin to code the uninformed Search Strategies:
Breadth First Search
public static void Breadth_First_Search(Node Start, Node Goal)
{
GetSucc x = new GetSucc();
ArrayList children = new ArrayList();
Queue Fringe = new Queue();
Fringe.Enqueue(Start);
while (Fringe.Count != 0)
{
Node Parent = (Node)Fringe.Dequeue();
Console.WriteLine("Node {0} Visited ", Parent.State);
if (Parent.State == Goal.State)
{
Console.WriteLine();
Console.WriteLine("Find Goal " + Parent.State);
break;
}
children = x.GetSussessor(Parent.State);
for (int i = 0; i < children.Count; i++)
{
int State = (int)children[i];
Node Tem = new Node(State, Parent);
Fringe.Enqueue(Tem);
}
}
}
Uniform Cost Search
public static void Uniform_Cost_Search(Node Start,Node Goal)
{
GetSucc x = new GetSucc();
ArrayList children = new ArrayList();
PriorityQueue Fringe = new PriorityQueue();
Fringe.Enqueue(Start);
while (Fringe.Count != 0)
{
Node Parent = (Node)Fringe.Dequeue();
Console.WriteLine("Node {0} Visited with Cost {1} ",
Parent.State,Parent.Cost);
if (Parent.State == Goal.State)
{
Console.WriteLine();
Console.WriteLine("Find Goal " + Parent.State);
break;
}
children = x.GetSussessor(Parent.State,Parent);
for (int i = 0; i < children.Count; i++)
{
Fringe.Enqueue((Node)children[i]);
}
}
}
Depth First Search
public static void Depth_First_Search(Node Start, Node Goal)
{
GetSucc x = new GetSucc();
ArrayList children = new ArrayList();
Stack Fringe = new Stack();
Fringe.Push(Start);
while (Fringe.Count != 0)
{
Node Parent = (Node)Fringe.Pop();
Console.WriteLine("Node {0} Visited ", Parent.State);
Console.ReadKey();
if (Parent.State == Goal.State)
{
Console.WriteLine();
Console.WriteLine("Find Goal " + Parent.State);
break;
}
children = x.GetSussessor(Parent.State);
for (int i = 0; i < children.Count; i++)
{
int State = (int)children[i];
Node Tem = new Node(State, Parent);
Fringe.Push(Tem);
}
}
}
Depth Limited Search
public static void Depth_Limited_Search(Node Start, Node Goal, int depth_Limite)
{
GetSucc x = new GetSucc();
ArrayList children = new ArrayList();
Stack Fringe = new Stack();
Fringe.Push(Start);
while (Fringe.Count != 0)
{
Node Parent = (Node)Fringe.Pop();
Console.WriteLine("Node {0} Visited ", Parent.State);
if (Parent.State == Goal.State)
{
Console.WriteLine();
Console.WriteLine("Find Goal " + Parent.State);
break;
}
if (Parent.depth == depth_Limite)
{
continue;
}
else
{
children = x.GetSussessor(Parent.State);
for (int i = 0; i < children.Count; i++)
{
int State = (int)children[i];
Node Tem = new Node(State, Parent);
Fringe.Push(Tem);
}
}
}
}
Iterative Deepening Search
public static void Iterative_Deepening_Search(Node Start, Node Goal)
{
bool Cutt_off = false;
int depth = 0;
while(Cutt_off == false)
{
Console.WriteLine("Search Goal at Depth {0}",depth);
Depth_Limited_Search(Start, Goal, depth,ref Cutt_off);
Console.WriteLine("-----------------------------");
depth++;
}
}
public static void Depth_Limited_Search(Node Start, Node Goal,
int depth_Limite,ref bool Cut_off)
{
GetSucc x = new GetSucc();
ArrayList children = new ArrayList();
Stack Fringe = new Stack();
Fringe.Push(Start);
while (Fringe.Count != 0)
{
Node Parent = (Node)Fringe.Pop();
Console.WriteLine("Node {0} Visited ", Parent.State);
if (Parent.State == Goal.State)
{
Console.WriteLine();
Console.WriteLine("Find Goal " + Parent.State);
Cut_off = true;
break;
}
if (Parent.depth == depth_Limite)
{
continue;
}
else
{
children = x.GetSussessor(Parent.State);
for (int i = 0; i < children.Count; i++)
{
int State = (int)children[i];
Node Tem = new Node(State, Parent);
Fringe.Push(Tem);
}
}
}
}
Bidirectional Search
public static void Bidirectional_Search(Node Start,Node Goal)
{
GetSucc x = new GetSucc();
ArrayList Children_1 = new ArrayList();
ArrayList Children_2 = new ArrayList();
Queue Fringe_IN = new Queue();
Queue Fringe_GO = new Queue();
Fringe_IN.Enqueue(Start);
Fringe_GO.Enqueue(Goal);
while((Fringe_IN.Count !=0)&&(Fringe_GO.Count!=0))
{
Node Parent1 = (Node)Fringe_IN.Dequeue();
Console.WriteLine("Node {0} Visited ", Parent1.State);
if ((Parent1.State == Goal.State)||Contain(Fringe_GO,Parent1))
{
Console.WriteLine();
Console.WriteLine("Find Goal " + Parent1.State);
break;
}
Children_1 = x.GetSussessor(Parent1.State);
for (int i = 0; i < Children_1.Count; i++)
{
int State = (int)Children_1[i];
Node Tem = new Node(State, Parent1);
Fringe_IN.Enqueue(Tem);
}
Node Parent2 = (Node)Fringe_GO.Dequeue();
Console.WriteLine("Node {0} Visited ", Parent2.State);
if ((Parent2.State == Start.State) || Contain(Fringe_IN,Parent2))
{
Console.WriteLine();
Console.WriteLine("Find Goal " + Parent2.State);
break;
}
Children_2 = x.GetSussessor_Reverse(Parent2.State);
for (int i = 0; i < Children_2.Count; i++)
{
int State = (int)Children_2[i];
Node Tem = new Node(State, Parent2);
Fringe_GO.Enqueue(Tem);
}
}
}
public static bool Contain(Queue Fringe,Node Parent)
{
object[] S = new object[Fringe.Count];
S = Fringe.ToArray();
for (int i = 0; i < S.Length; i++)
{
Node Target = (Node)S[i];
if (Target.State == Parent.State)
{
return true;
}
}
return false;
}
Reference
- Stuart Russell, Peter Norving, Artificial Intelligence: A Modern Approach
